标签:
Daoyi Peng
May 22, 2014
Ptolemy 定理 圓內接四邊形的對角線長度之積等於兩組對邊長度乘積之和.
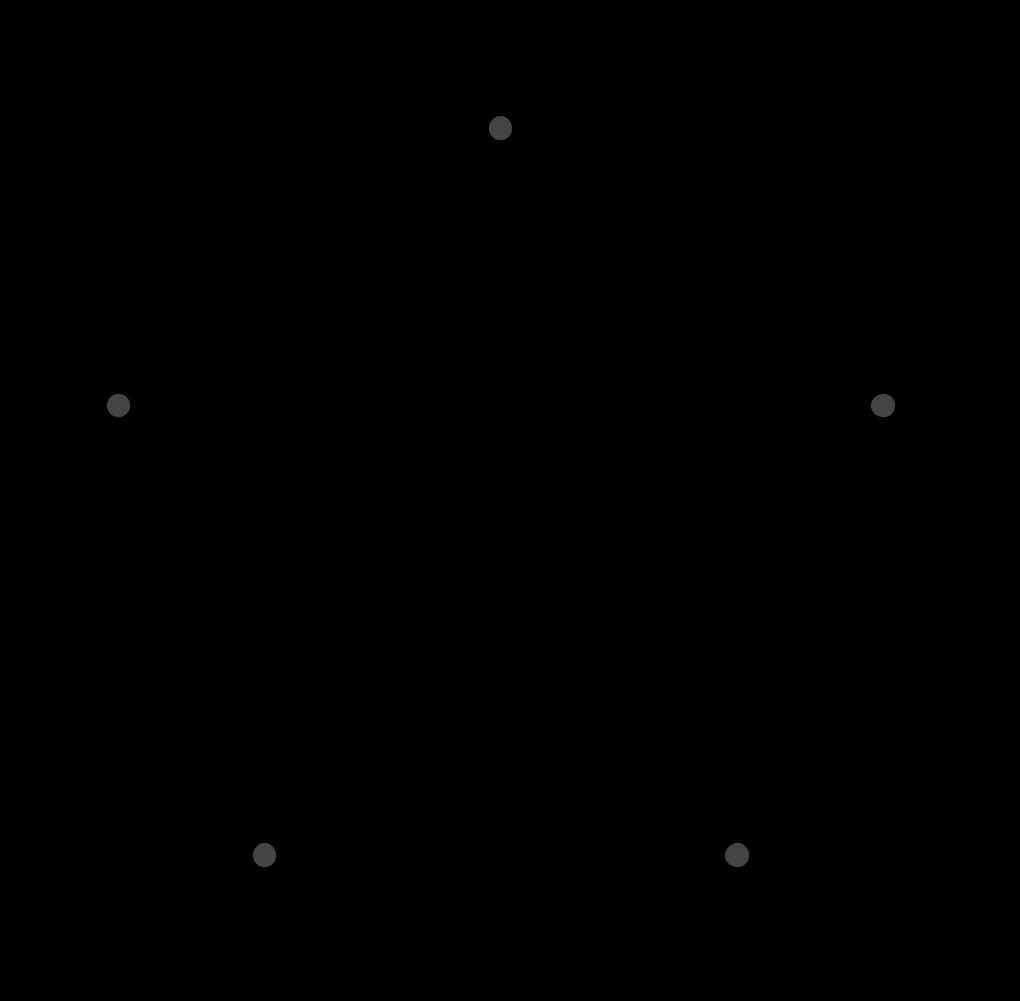
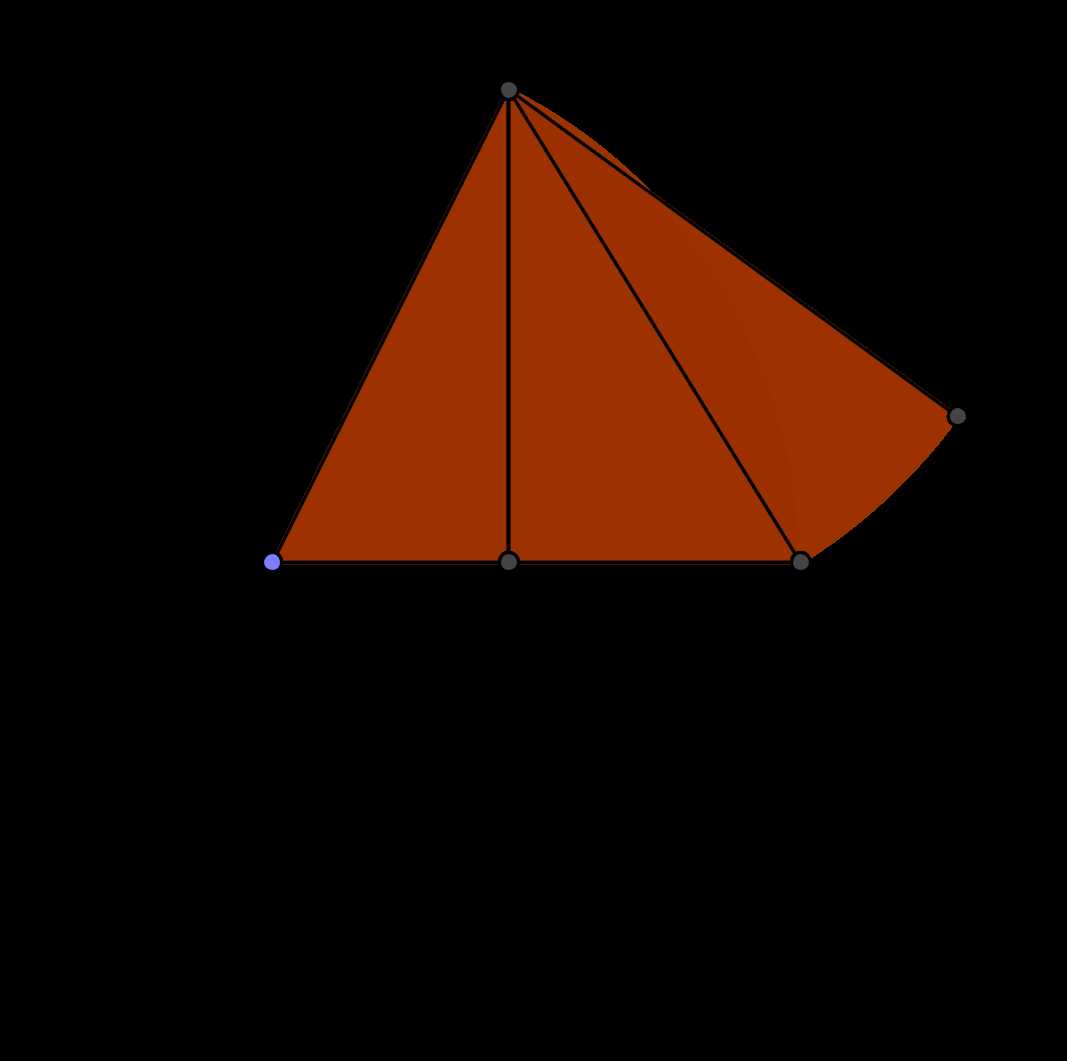
Fig 1 為正五邊形 $ABCDE$, 考慮圓內接四邊形 $ABDE$, 其中 $|AB|=|AE|=|ED|=a$, $|BD|=|AD|=|BE|=b$, 由 Ptomlemy 定理, 有
\[|AB|\cdot |ED| +|AE|\cdot |BD| = |AD|\cdot |BE|.\]
即得
\[a^2+ab=b^2.\]
注意到 $\displaystyle a=2R\sin\frac{\pi}{5}, b=2R\sin\frac{2\pi}{5}$, 從而
\[4R^2 \sin^2\frac{\pi}{5} + 4R^2 \sin\frac{\pi}{5}\sin\frac{2\pi}{5} =4R^2 \sin^2\frac{2\pi}{5},\]
使用倍角公式 $\displaystyle \sin\frac{2\pi}{5}=2\sin\frac{\pi}{5}\cos\frac{\pi}{5}$, 上式化為
\[1+ 2\cos\frac{\pi}{5} = 4\cos^2\frac{\pi}{5}.\]
解得
\[\cos\frac{\pi}{5}=\frac{\sqrt{5}+1}{4}.\]
於是
\[\sin\frac{\pi}{5} = \frac{\sqrt{10-2\sqrt{5}}}{4}. \]
只需尺規作出長度為 $\sqrt{10-2\sqrt{5}}$, 即可得到正五邊形.
下面給出正五邊形尺規作圖過程.
Fig 2 中, 作圓 $O$, 易做兩垂直的直徑, 點 $B$ 為所在半徑的中點, 以 $AB$ 長為半徑, $B$ 為圓心畫弧, 交直徑于點 $C$. 以 $A$ 為圓心, $AC$ 長為半徑作圓弧, 交圓 $O$ 于 $D$ 點. $AD$ 長即為圓 $O$ 內接正五邊形的邊長.
\[|AO|=2,\ |BO|=1,\ |AB|=|BC|=\sqrt{5},\ |OC|=\sqrt{5}-1,\ |AC|=\sqrt{10-2\sqrt{5}}.\]
标签:
原文地址:http://www.cnblogs.com/pengdaoyi/p/4287002.html