标签:
题目:
Given a string S and a string T, count the number of distinct subsequences of T in S.
A subsequence of a string is a new string which is formed from the original string by deleting some (can be none) of the characters without disturbing the relative positions of the remaining characters. (ie, "ACE" is a subsequence of "ABCDE" while "AEC" is not).
Here is an example:
S = "rabbbit", T = "rabbit"
Return 3.
思路与实现:
题目的意思如下:给定字符串S和T,求S的子串中与T相同的个数。注意子串是在原字符串中删除某些字符得到的字符串。如“ACE”是“ABCDE”的子串,而“AEC”不是,因为“AEC”把原字符串中的顺序改变了。
很明显这是一道动态规划的题。首先需要找到递推关系。
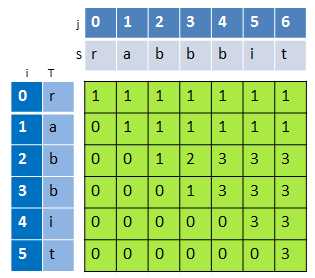
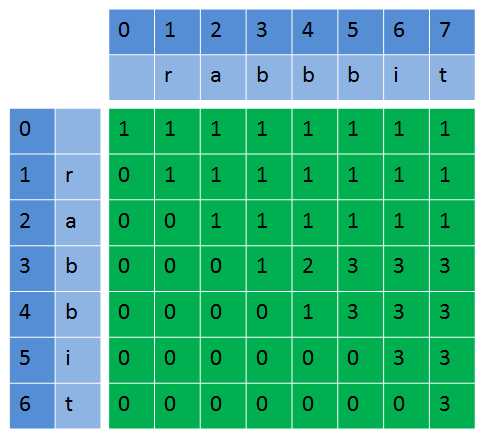
假设原字符S的长度为i,子字符串T的长度为j,用dp[i-1][j-1]表示S中含T的个数。例如:S="r",T="r",d[1-1][1-1] = d[0][0] = 1;S="ra",T="r",d[1][0] = 1。对于S="rabbbit",T="rabbit",可以得到一个如下的二维数组:(如下第三个图)
先看第一个图,对于dp[0][0],即S="r",T="r",dp[0][0]=1,若第一个字符不等,则dp[0][0]=0;对于dp[0][1],即S="ra",T="r",dp[0][1]=1;同理可以得出第一行都是1。
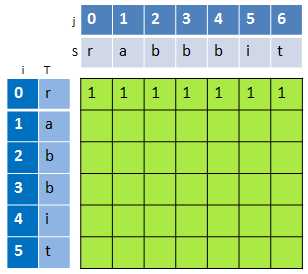
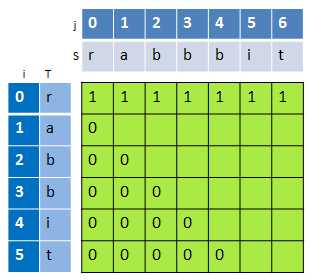
如下图,当i>j时,dp[i][j]=0,因此,对于第一列(i=0),除了dp[0][0]需要根据S[0]是否等于T[0]来确定之外,其他的dp[0][j]都为0。
填充整个二维数组。对于i=j,dp[i][j]不会超过1。
从这个二维数组可以看出,可以得出如下的递推关系(注意这个i,j):
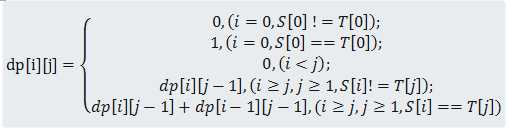
构造一个二维数组来实现算法:
class Solution {
public:
int numDistinct(string S, string T) {
int ls = S.length();
int lt = T.length();
if(lt > ls || ls == 0)return 0;
static int dp[1000][1000] = {0};
int i,j;
for(i = 0; i < lt; i++)
for(j = 0; j < ls; j++)
dp[i][j] = 0;
if(S[0] == T[0]){
for(j = 0; j < ls; j++){
dp[0][j] = 1;
}
}
for(i = 1; i < lt; i++){
for(j = i; j < ls; j++){
if(T[i] == S[j])dp[i][j] = dp[i][j-1] + dp[i-1][j-1];
else dp[i][j] = dp[i][j-1];
}
}
int r = dp[lt-1][ls-1];
return r;
}
};
这样提交之后发现"ccc", "c"这个case通不过,看来对于i=0的情况还要特殊处理。修改之后,如下,但是会超时。所以只能想别的办法。
public:
int numDistinct(string S, string T) {
int ls = S.length();
int lt = T.length();
if(lt > ls || ls == 0)return 0;
static int dp[11000][11000] = {0};
int i,j;
for(i = 0; i < lt; i++)
for(j = 0; j < ls; j++)
dp[i][j] = 0;
if(S[0] == T[0])dp[0][0] = 1;
for(j = 1; j < ls; j++){
if(S[j] == T[0])
dp[0][j] = dp[0][j-1] + 1;
else
dp[0][j] = dp[0][j-1];
}
for(i = 1; i < lt; i++){
for(j = i; j < ls; j++){
if(T[i] == S[j])dp[i][j] = dp[i][j-1] + dp[i-1][j-1];
else dp[i][j] = dp[i][j-1];
}
}
int r = dp[lt-1][ls-1];
return r;
}
下面这样处理比较好,就不需要对i=0的情况做特殊处理,相当于在S和T前加一个空字符。初始化的时候dp[0][j]=1(0<=j<=S.size());dp[i][0]=0(1<=i<=T.size())。
未完--待续
[leetcode]Distinct Subsequences
标签:
原文地址:http://www.cnblogs.com/zhutianpeng/p/4288340.html