标签:
题意:给出一个长为a,宽为b的布,再给出n个围巾的规格(长x,宽y,价值c),问怎样裁剪能够得到最大的价值。
----第一次做的时候不会---然后放到今天做--发现还是不会---于是又--看题解了----@_@===
因为相同规格的围巾可以重复剪多次,且围巾的长和宽相当于两个约束,所以可以转换为二维费用的完全背包问题。
然后就是围巾的裁剪
第一种 横着减
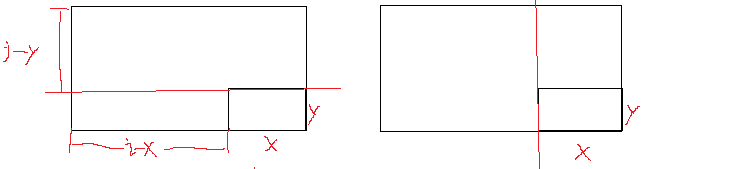
裁切线分为两种
对于左上的第一个图,当减去长为x,宽有长为y的一个矩形之后,剩余的面积之和分别由长为i-x,宽为y;长为i,宽为j-y的两个矩形组成。
对于左上的第二个图,当减去长为x,宽有长为y的一个矩形之后,剩余的面积之和分别由长为i-x,宽为j;长为x,宽为j-y的两个矩形组成。
第二种 竖着减 和第一种的方法类似--
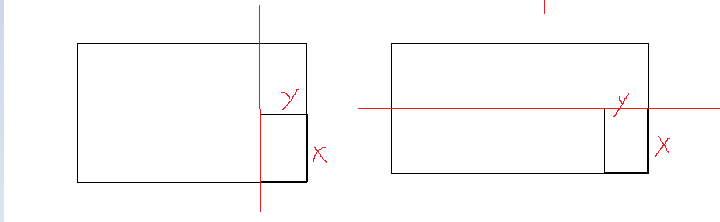
然后就可以写出状态转移方程----

#include<iostream> #include<cstdio> #include<cstring> #include<algorithm> #define maxn 1005 using namespace std; struct node { int x,y,c; } a[maxn]; int dp[maxn][maxn]; int main() { int ncase,n,c,d,i,j,k; scanf("%d",&ncase); while(ncase--) { scanf("%d %d %d",&n,&c,&d); for(i=0;i<n;i++) scanf("%d %d %d",&a[i].x,&a[i].y,&a[i].c); memset(dp,0,sizeof(dp)); for(i=0;i<=c;i++) { for(j=0;j<=d;j++) { for(k=0;k<n;k++) { if(i>=a[k].x&&j>=a[k].y) dp[i][j]=max(dp[i][j],max(dp[i-a[k].x][a[k].y]+dp[i][j-a[k].y]+a[k].c,dp[i-a[k].x][j]+dp[a[k].x][j-a[k].y]+a[k].c)); if(i>=a[k].y&&j>=a[k].x) dp[i][j]=max(dp[i][j],max(dp[i-a[k].y][j]+dp[a[k].y][j-a[k].x]+a[k].c,dp[i][j-a[k].x]+dp[i-a[k].y][a[k].x]+a[k].c)); } } } printf("%d\n",dp[c][d]); } }
标签:
原文地址:http://www.cnblogs.com/wuyuewoniu/p/4290545.html