标签:
【转载请注明出处】http://www.cnblogs.com/mashiqi
在回归问题中,偶尔我们会遇到求方差的估计的情况。举了例子,我们常常通过Gaussian分布${\cal N}(\mu ,{\sigma^2})$的样本集合$\{x_i\}_{i=1}^n$去估计分布的参数$\mu,\sigma^2$。对$\mu$的估计应该大家都很熟悉了:$\hat{\mu}=\bar{x} \sum_{i=1}^n x_i$,然而,对$\sigma^2$的估计,在教科书中,却常常见到两种形式:
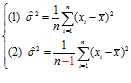
第一种形式就不解释了,第二种形式一般称为对$\sigma^2$的无偏估计形式。这是除以$n-1$才是无偏的呢?这个问题往往是刚接触的同学的困惑。不过这个$n-1$似乎也不是那么的天外来客:你看,$\bar{x}$与$x_i$并不是独立的,这必然导致每一个求和项$(x_1-\bar{x}),(x_2-\bar{x}),\cdots,(x_n-\bar{x})$之间并不是完全的独立的关系,因此求和之后直接除以$n$肯定不对啊,要调整,这个调整就是减一:$n \rightarrow n-1$。以上是一个make sense的解释,相信大家听了过后就会理解为什么要减一了。但是处女座同学和强迫症患者往往不会仅仅满足于此(裤子都脱了,你就给我说这些!?),所以,下面就给一个mathematical的解释。
RSS(Residual Sum of Squares)的定义是:
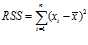
其中$\bar{x} = \frac{1}{n} \sum_{i=1}^n x_i$是平均值。我们的目标是没有蛀牙把$RSS$转化成一个个相互独立的项然后求和。
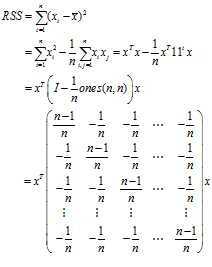
我们记最后的中间的这个矩阵为$A$,由于$A$是实对称的,因此肯定和对角矩阵合同。对$A$进行对角分解得:
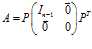
其中$P$是正交矩阵。于是有
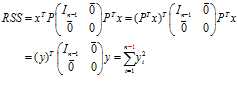
其中$y=P^Tx$。我们现在来检查一下$y$的方差(假设$Ex=0$):
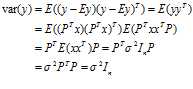
因此$y$的各个分量$\{y_i\}_{i=1}^n$之间相互独立,并且方差为$\sigma^2$。所以从式来看,$RSS/(n-1)$确实是对$\sigma^2$的一个不错的估计(无偏的)!
正交矩阵$P$是怎么得到的呢?

$\lambda=0$对应的单位特征向量为$(1/\sqrt{n},1/\sqrt{n},\cdots,1/\sqrt{n})^T$;
$\lambda=1$对应的$n-1$个单位特征向量为$p_i$,其中$p_i \in \{\alpha \in \mathcal{R}^n|(1,1,\cdots,1)\alpha=0,||\alpha||_2=1\}$,并且$p_i,p_j$之间相互垂直。
经过我抓耳挠腮的推导后,求出$p_i$是这样的(大家拿去用吧不用感谢我/羞):
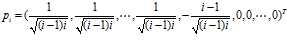
其中$p_i$的前$i-1$个分量是$\frac{1}{\sqrt{(i-1)i}}$,第$i$个分量是$-\frac{i-1}{\sqrt{(i-1)i}}$,后面的就算是0。其中需要专门给出的是$p_i=(\frac{1}{\sqrt{2}},-\frac{1}{\sqrt{2}},0,\cdots,0)$。因此:
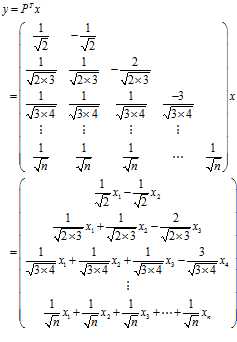
因此,$x$和$y$之间的对应关系就是:
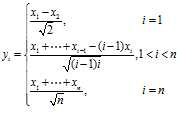
补充内容:
$$\sum_{i=1}^n (x_i - \bar{x})^2 = \sum_{i=1}^n x_i^2 - \frac{1}{n} \sum_{i,j=1}^n x_i x_j = \frac{1}{2n} \sum_{i,j=1}^n (x_i - x_j)^2$$
PS:今天情人节,也不知道她过的怎样呢?禁止其他男生给她送礼物!!!
RSS(Residual Sum of Squares)的自由度为什么是n-1呢
标签:
原文地址:http://www.cnblogs.com/mashiqi/p/4291520.html