标签:
一、CRC的作用
CRC的英文全称为Cyclic Redundancy Check(Code),中文名称为循环冗余校验(码)。它是一类重要的线性分组码,编码和解码方法简单,检错和纠错能力强,在通信领域广泛地用于实现差错控制。
二、CRC的原理
(一)CRC的校验过程描述
1、 被校验的原数据转换成二进制序列,假设共K位
2、 以一定规则产生一个新的二进制序列,假设共R位的。
3、 把新的二进制序列附加在原数据二进制序列后面,共K+R位,发送出去。
4、 接收端接收数据后,把原数据的K位二进制序列按相同规则产生一个R位二进制序列与附加的R位二进制序列进行比较,相同表示传递的数据没有问题,不相同表示传递的数据出现错误与误差。
(二)CRC的校验码生成过程描述 其中对二进制序列的转换规则是CRC中的关键。
校验规则规则描述如下:
1、首先把原数据二进制序列可以看成一个多项式,比如10011看成多项式x4+x1+1,其中多项式系数只能是0,1。
2、然后定义一个规则,也是使用多项式,这个多项式专业名称叫生成多项式。其系数也只能是0,1。
3、使用原数据对应的多项式除以生成多项式,得到一个余数多项式。其系数也只能是0,1。
4、余数多项式的系数转换成一个二进制,这就是CRC校验码。
(三)CRC生成多项式说明 根据不同的需求,生成多项式有多种类型,说明如下表:
| 名称 | 生成多项式 |
| CRC-4 | x4+x1+1 |
| CRC-8 | x8+x2+x1+1 |
| CRC-12 | x12+x11+x3+x2+x1+1 |
| CRC-16 | x16+x15+x2+1 |
| CRC-ITU | x16+x15+x5+1 |
| CRC-32 | x32+x26+x23+x22+x16+x12+x11+x10+x8+x7+x5+x4+x2+x1+1 |
CRC-32使用的就是上面最高指数为32的多项式,对应的二进制序列是
100000100110000010001110110110111。
(四)CRC多项式除法规则
在一般的除法中,都使用的是减运算,但在CRC多项式除法运算中使用的是异或运算。
(五)CRC原理实例说明
下面使用一个实例说明校验码生成及其除法规则。
已知原始数据的二进制序列是1010,采用的生成多项式是CRC-8类型100000111。原始数据对应的多项式是t(x)=x3+x1,生成多项式是G x =x8+x2+x1+1。
大家可以看到上面的一个现象,就是不用除了,原数据对应的二进制序列对应的多项式就已经是余数多项式了,这样CRC运算就没有意义了。所以要保证每一位都能进行运算,需要对在原始数据的二进制序列后加若干0,0的个数由生成多项式的最高指数(阶数)决定,这里就是补充8个0,原数据二进制序列变成101000000000,对应对多项式就是x8t x =x11+x9。这样可以保证CRC除法至少进行一次。
除法过程如下图示:

结果是110110,对应多项式是x5+x4+x2+x1
校验码是110110。
(六)CRC的算法
上面的原理转换成程序还是比较难的,所以需要把上面过程转换成算法,同时在该算法基础上提出了很多优化算法,比如查表算法。
计算机硬件已经实现了CRC的算法,对CRC-8其中使用寄存器8个,异或运算三个。因为CRC-8 的生成多项式是,其中R0表示常数项1,R1表示,R2表示。多项式中的连续两项之间对应一个异或运算。记住R7到R0是连续的两项。
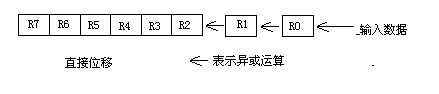
R0,R1,R2,R3,R4,R5,R6,R7是8个寄存器,如果采用32,需要32个寄存器。其中的异或运算的位置根据生成多项式来确定。
下面八上面的图示的过程转换成算法描述:
1、 寄存器全部初始化为0。
2、 每次位移全部进行。
3、 其中的异或操作的输入需要两个位,其中一位是R7的移出位,另外一个就是右边的异或运算输出。
4、 结束条件是原数据位都进行了输入。
运算步骤过程图示:
输入原数据二进制序列101000000000,每个位输入完毕,则算法完毕。
|
移出 |
寄存器R7-R2 |
xor |
R1 |
xor |
R0 |
xor |
输入 |
|||||
|
<= |
0 |
0 |
0 |
0 |
0 |
0 |
|
0 |
|
0 |
|
|
|
0 |
0 |
0 |
0 |
0 |
0 |
0 |
<=0+0 |
0 |
<=0+0 |
1 |
<=0+1 |
1 |
|
0 |
0 |
0 |
0 |
0 |
0 |
0 |
<=0+0 |
1 |
<=0+1 |
0 |
<=0+0 |
0 |
|
0 |
0 |
0 |
0 |
0 |
0 |
1 |
<=0+1 |
0 |
<=0+0 |
1 |
<=0+1 |
1 |
|
0 |
0 |
0 |
0 |
0 |
1 |
0 |
<=0+0 |
1 |
<=0+1 |
0 |
<=0+0 |
0 |
|
0 |
0 |
0 |
0 |
1 |
0 |
1 |
<=0+1 |
0 |
<=0+0 |
0 |
<=0+0 |
0 |
|
0 |
0 |
0 |
1 |
0 |
1 |
0 |
<=0+0 |
0 |
<=0+0 |
0 |
<=0+0 |
0 |
|
0 |
0 |
1 |
0 |
1 |
0 |
0 |
<=0+0 |
0 |
<=0+0 |
0 |
<=0+0 |
0 |
|
0 |
1 |
0 |
1 |
0 |
0 |
0 |
<=0+0 |
0 |
<=0+0 |
0 |
<=0+0 |
0 |
|
1 |
0 |
1 |
0 |
0 |
0 |
1 |
<=1+0 |
1 |
<=1+0 |
1 |
<=1+0 |
0 |
|
0 |
1 |
0 |
0 |
0 |
1 |
1 |
<=0+1 |
1 |
<=0+1 |
0 |
<=0+0 |
0 |
|
1 |
0 |
0 |
0 |
1 |
1 |
0 |
<=1+1 |
1 |
<=1+0 |
1 |
<=1+0 |
0 |
|
0 |
0 |
0 |
1 |
1 |
0 |
1 |
<=0+1 |
1 |
<=0+1 |
0 |
<=0+0 |
0 |
|
结果 |
0 |
0 |
1 |
1 |
0 |
1 |
|
1 |
|
0 |
|
|
注意其中+是异或运算,异或运算就是不进位的加法。
结果与前面多项式余数一样都是110110
(七)纠错
在接收端收到了CRC码后用生成多项式为G(x)去做模2除,若得到余数为0,则码字无误。若如果有一位出错,则余数不为0,而且不同位出错,其余数也不同。可以证明,余数与出错位的对应关系只与码制及生成多项式有关,而与待测碼字(信息位)无关。图10给出了G(x)=1011,C(x)=1010的出错模式,改变C(x)(码字),只会改变表中码字内容,不改变余数与出错位的对应关系。
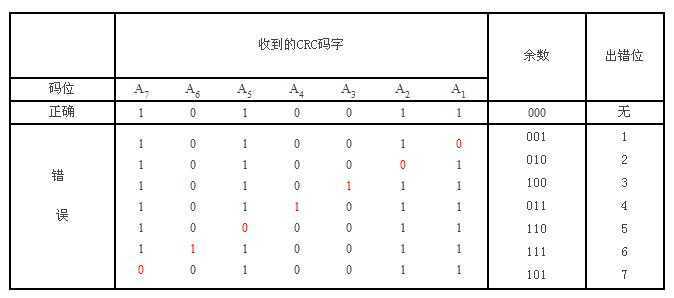
图10 (7,4)CRC码的出错模式(G(x)=1011)
如果循环码有一位出错,用G(x)作模2除将得到一个不为0的余数。如果对余数补0继续除下去,我们将发现一个有趣的结果;各次余数将按图10顺序循环。例如第一位出错,余数将为001,补0后再除(补0后若最高位为1,则用除数做模2减取余;若最高位为0,则其最低3位就是余数),得到第二次余数为010。以后继续补0作模2除,依次得到余数为100,0ll…,反复循环,这就是“循环码”名称的由来。这是一个有价值的特点。如果我们在求出余数不为0后,一边对余数补0继续做模2除,同时让被检测的校验码字循环左移。图10说明,当出现余数(101)时,出错位也移到A7位置。可通过异或门将它纠正后在下一次移位时送回A1。这样我们就不必像海明校验那样用译码电路对每一位提供纠正条件。当位数增多时,循环码校验能有效地降低硬件代价,这是它得以广泛应用的主要原因。
关于生成多项式,并不是任何一个r次的多项式都可以作为生成多项式。从检错及纠错的要求出发,生成多项式应能满足下列要求:
(1) 任何一位发生错误应当使余数不为0;
(2) 不同位发生错误应当使余数不同;
(3) 对余数继续作模2除,应使余数循环。
将这些要求反映为数学关系是比较复杂的,对一个(n,k)码来说,可将(xn -1)分解为若干质因子式(注意是模2运算),根据编码所要求的码距,选取合适的r值,选其中的一个因式或若干因式的乘积作为生成多项式,为r次多项式,且最高、最低位系数均为1。
例: x7-1=( x+1)(x3+x+1)(x3+x2+1) (模2运算)
选择 G(x)= x+1 = 11,可构成(7,6)码,只能判一位错。
选择 G(x)= x3+x+1=1011,或 x3+x2+1=1101,可构成(7,4)码,能判两位错或纠一位错。
选择 G(x)=(x+1)(x3+x+1)=11101,可构成(7,3)码,能判两位错并同时纠正一位错。
对使用者来说,可从有关资料上查到对应于不同码制的生成多项式,表2.5仅给出了一部分。
【例】(G(x)=1011,C(x)=1010)(7,4)码(总共7位,信息位4)
CRC校验码:
补齐7位
1010000
1011
0001000
1011
0011
传输1010011
如果第6位出错
1010001
1011
0001001
1011
0010
【例】(G(x)=1101,C(x)=1010)(7,4)码(总共7位,信息位4)
补齐七位
1010000
1101
0111000
1101
001100
1101
0001
传输1010001
1010001
1101
0111001
1101
001101
1101
0000
如果第6位出错
1010011
1101
0111011
1101
001111
1101
0010
补零继续模2除
补1位
0100(最高位为0,余数为后三位100)
1000(最高位为1,做模2除)
1101
0101(余数为101)
1010
1101
0111(余数为111)
标签:
原文地址:http://www.cnblogs.com/javaleon/p/4291939.html