标签:
问题陈述:
给定N个整数的序列{A1, A2, ... , AN},求函数ƒ(i, j) = max{0, Ai + Ai+1 + ... + Aj}(1<=i<j<=N)的最大值。
问题分析:
求给定数列的最大子列和。
算法设计:
算法1:计算每个子列的和
时间复杂度: T(N) = O(N2)
1 int MaxSubSeqSum(int arr[], int n) { 2 int i, j, currentSum, maxSum = 0; 3 for(i=0; i<N-1; i++) { /* i是子列左端的位置 */ 4 currentSum = 0; /* currentSum是从A[i]到A[j]的子列和 */ 5 for(j=i; j<N; j++) { /* j是子列右端位置 */ 6 currentSum += arr[j]; 7 if(currentSum > maxSum){ 8 maxSum = currentSum; //更新maxSum 9 } 10 } 11 } 12 return maxSum; 13 }
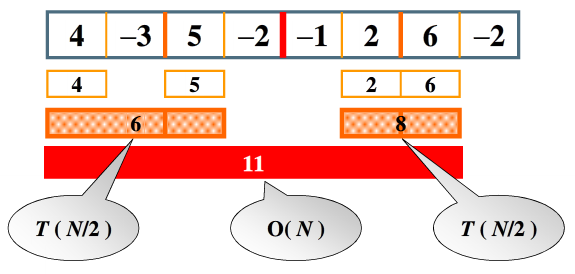
算法2:递归 分而治之
将数列分为两部分,分别求出左右两侧的最大子数列,再求出跨越分界线的最大子数列,比较三者最大值即为所求的最大子数列。
时间复杂度: T(N) = O(NlogN)
1 int MaxSubSeqSum(int arr[], int left, int right) { 2 if(left == right){ 3 if(arr[left] > 0){ 4 return arr[left]; 5 }else { 6 return 0; 7 } 8 } 9 10 int center = (left + right) / 2; 11 int leftMaxSum = MaxSubSeqSum(arr, left, center); /* 分界线左侧最大子数列 */ 12 int rigthMaxSum = MaxSubSeqSum(arr, center+1, right); /* 分界线右侧最大子数列 */ 13 14 /* 以分界线往左求最大子数列 */ 15 int leftBorderSum = 0, maxLeftBorderSum = 0; 16 for(int i=center; i>=left; i--) { 17 leftBorderSum += arr[i]; 18 if(leftBorderSum > maxLeftBorderSum){ 19 maxLeftBorderSum = leftBorderSum; 20 } 21 } 22 23 /* 以分界线往右求最大子数列 */ 24 int rightBorderSum = 0, maxRightBorderSum = 0; 25 for(int j=center+1; j<=right; j++) { 26 rightBorderSum += arr[j]; 27 if(rightBorderSum > maxRightBorderSum) { 28 maxRightBorderSum = rightBorderSum; 29 } 30 } 31 32 /* 跨越分界线最大子数列和 */ 33 int maxBorderSum = maxLeftBorderSum + maxRightBorderSum; 34 35 return maxSum(leftMaxSum, rigthMaxSum, maxBorderSum); 36 } 37 38 /* 39 ** 返回a, b, c三者最大值 40 */ 41 int maxSum(int a, int b, int c){ 42 if(a > b) { 43 a = b; 44 } 45 if(a > c) { 46 return a; 47 }else { 48 return c; 49 } 50 }
时间复杂度计算:
T(N) = 2 * T(N/2) + cN
= 22 * T(N/22) + c2N
= 2k * T(N/2k) + ckN 其中 N/2k = 1
= N * T(1) + cNlog2N
= O(NlogN)
算法3:在线处理(每输入一个数据就进行即时处理)
时间复杂度: T(N) = O(N)
1 int MaxSubSeqSum(int arr[], int n) { 2 int currentSum, maxSum; 3 currentSum = maxSum = 0; 4 for(int i=0; i<n; i++) { 5 currentSum += arr[i]; /* 向右累加 */ 6 if(currentSum > maxSum) { /* 发现更大值 更新最大值 */ 7 maxSum = currentSum; 8 }else if(currentSum < 0){ /* 如果当前子列为负 舍弃 置零 */ 9 currentSum = 0; 10 } 11 } 12 return maxSum; 13 }
参考资料:浙江大学数据结构
转载请注明出处:http://www.cnblogs.com/michaelwong/p/4292936.html
标签:
原文地址:http://www.cnblogs.com/michaelwong/p/4292936.html