标签：
AVL是一种平衡的二叉树。它的作用是避免二叉树形成像链表那样的O(N)结构。
条件：每个节点左子树与右子树的高度最多差1。
我们在进行插入与删除时会改变其平衡性，于是引入旋转：
旋转：
对于需要重新平衡的那个点A来说，分为四种情况：
① 捣乱的在A左儿子的左子树
② 捣乱的在A左儿子的右子树
③ 捣乱的在A右儿子的左子树
④ 捣乱的在A右儿子的右子树
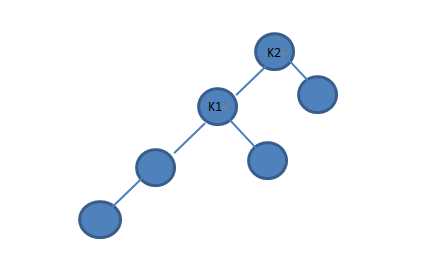比如K2即为A点，捣乱的那个点我们定义为K1的左子节点（反正我们就看需要平衡那个点高度较高的子树：是在左边的左边还是左边的右边balabala）
树的定义：
1 typedef struct AvlNode *AvlTree; 2 typedef struct AvlNode *Position; 3 4 struct AvlNode{ 5 int Element; 6 AvlTree left; 7 AvlTree right; 8 int Height; 9 };
单旋转k1成为新的顶点，想象着按着ｋ１左扭右扭
单左旋转用于①：
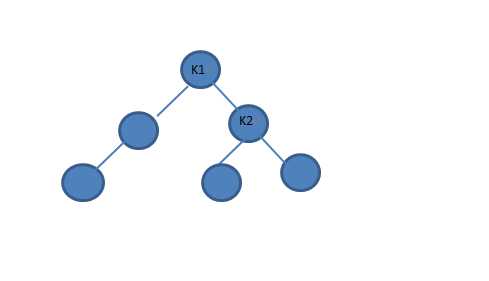
1 Position SingleRotateLeft(Position k2){ //单左旋转 2 Position k1 = k2->left; 3 k2->left = k1->right; 4 k1->right = k2; 5 k2->Height=(__max(Height(k1->left),k2->Height)+1); 6 k1->Height = (__max(Height(k2->left), Height(k2->right)) + 1); 7 return k1; //返回现在的顶点 8 9 }
单右旋转用于②：
1 Position SingleRotateRight(Position k2){ //单右旋转 2 Position k1 = k2->right; 3 k2->right = k1->left; 4 k1->left = k2; 5 k2->Height = (__max(Height(k1->right), k2->Height) + 1); 6 k1->Height = (__max(Height(k2->left), Height(k2->right)) + 1); 7 return k1; //返回现在的顶点 8 9 }
双旋转：
左-右旋转：（用于②）
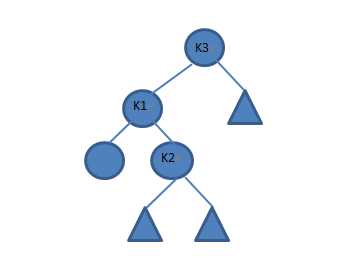
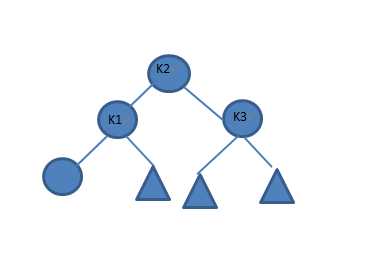
k3是需要重新平衡的那个点，先对k1-k2进行左转，再对k3-k2进行右转
1 Position DoubleRotateLeft(AvlTree k3){ //左子树的右子树插入 2 k3->left = SingleRotateRight(k3->left); 3 return SingleRotateLeft(k3); 4 }
右-左旋转：（用于③）
1 Position DoubleRotateRight(AvlTree k3){ //右子树的左子树插入 2 k3->right = SingleRotateLeft(k3->right); 3 return SingleRotateRight(k3); 4 }
插入：
对于下面那个递归算法：因为插入后只有从插入点到根节点的节点的平衡可能被改变，所以就沿着这条线进行递归更新：
疑惑：高度为H的AVL树最少节点数与最多节点数？
N个节点的AVL树的深度？
标签：
原文地址：http://www.cnblogs.com/stezqy/p/4293452.html
