标签:
并查集是一种数据结构,一般用来解决连通性或者动态连通性的问题。
动态连通性:
即一个图有n个结点,不断加入边,问此时任意两个结点的连通性。
建模思路:
对于连通的结点它们属于一个组,不连通的结点就属于不同的组。对于每一条边的输入,
判断两个结点是否连通,如果不连通则将两个结点所属的两个组连成一个组。对于每一个组,设置一个组标志。
初始时,任意两个结点不连通,组标志就是自己。
for(i=0; i<n; ++i) father[i] = i;
组的体现形式:
连通的结点属于一个组,那么组内是怎么体现的呢?
是用树来实现的
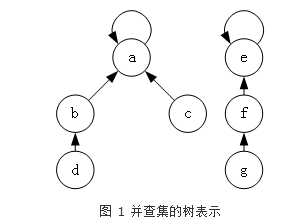
左边一个组,组的标志是a,右边一个组,组的标志是e
然后father[b] = a,father[c] = a, father[d] = d;
如果每个结点的终极祖先相同,那么就是一个组。
查找结点属于哪一个组的算法find
1 int find(int x) 2 { 3 if(x==parent[x]) return x;//如果自己的父亲是自己,那么就是这个组的标志 4 return find(parent[x]);//否则,看父亲的父亲是不是组的标志 5 }
如果输入一条边u-->v。如果u和v不属于一个组,那么就把两个组变成一个组
1 int Union(int u, int v) 2 { 3 int ru = find(u); 4 int rv = find(v); 5 if(ru != rv) 6 { 7 parent[ru] = rv; 8 } 9 }
但是会发生一个问题,那就是极端下,树的高度可能会很极端
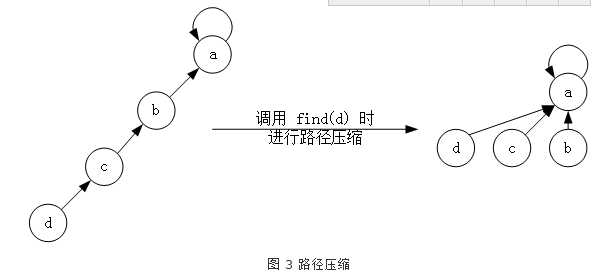
所以要进行路径压缩,即在find()函数返回的过程中,修改father数组
1 int find(int x) 2 { 3 if(x==parent[x]) return x;//如果自己的父亲是自己,那么就是这个组的标志 4 return parent[x] = find(parent[x]);//返回的过程中修改father数组,路径压缩 5 }
可是仍然存在问题,如果Union很多次,才find一次,那么极端情况下,情况仍然不理想,所以就存在按秩合并
低的树指向高的树,不会增加书高,即按秩合并
1 int Union(int u, int v) 2 { 3 int ru = find(u); 4 int rv = find(v); 5 if(ru != rv) 6 { 7 if(rank[ru] <= rank[rv]) 8 { 9 parent[ru] = rv; 10 if(rank[ru]==rank[rv]) 11 rank[rv]++; 12 } 13 else 14 parent[rv] = ru; 15 } 16 }
标签:
原文地址:http://www.cnblogs.com/justPassBy/p/4295439.html