标签:
Part I 起源:线性回归
线性回归很常见,给你一堆点,作出一条直线,尽可能去拟合这些点。对于多维的数据,设特征为xi,设函数h(θ)=θ+θ1x1+θ2x2+.....为拟合的线性函数,其实就是内积,实际上就是y=Wx+b。
那么如何确定这些θ参数(parament)才能保证拟合比较好呢?
①确定目标函数
我们易有这样的二次目标函数:J=min Σ 1/2(h(θ)-yi)^2 ,i:1~m,即所有数据条数。
该目标函数的意义在于:误差最小化。
h(θ) 中的h即是hypothesis(假设的意思),h函数是我们的算出结果,yi是我们的实际结果,平方的作用有两个,一是是代替ABS,二方便求导。
②梯度下降算法
计算机是很笨的。如果想要确定某个值,那么有一种很笨的方法:迭代法。
设定一个边界初值(最大or最小),然后一小步一小步的去变化这个值并验证,知道最后逼近最优值,停止迭代。
由于目标函数是最小化,我们有这个算法。
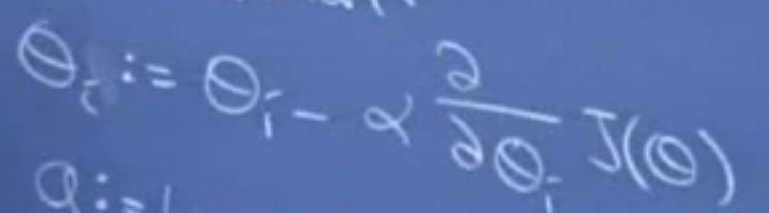
首先把各个θ设为比较大的值,然后不停迭代,让其减小。
减小的量由alpha(步长,0.01即可)*目标函数J的偏导数构成。
偏导数意义上就是梯度(高数内容),也就是函数下降的快慢。
调整各个θ的同时,目标函数J的计算值也在减小。
同时梯度的下降速度由疾变缓,在最后的迭代过程中,梯度将会趋于0,从而能够保证较为精确的逼近目标值。这样,既保证了目标函数的最小化,又求出的参数θ。
③偏导数的处理
假设只有一条数据。目标函数J的偏导数你可以化简一下。链式法则求导。
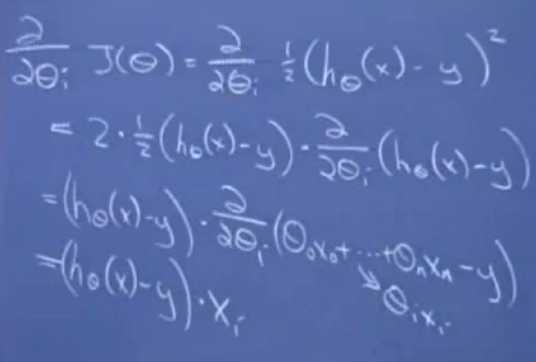
最后的求导结果是一个非常神奇的式子:(h(θ)-y)*xi
如果是多条数据呢?推导的结果是这个玩意。
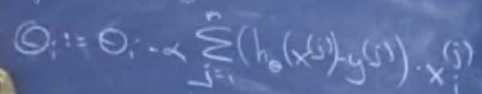
由此诞生了两种梯度算法。
一、批梯度算法。
正如上面的式子,每次迭代确定每个维度的偏导结果时,扫一下全部数据的全部维度。
需要3个for。下场是:慢。
二、随机梯度算法。
它的改良就是,算当前维度的偏导结果时,不要遍历数据集全部维度了,只算当前维度的。
for(..维度)
for(数据条数)
Θi=Θi-alpha*(h(Θ)-yj)*x[i]
PS. 关于常量b的求法=Σ alpha*(h(Θ)-yj)
这种算法偷工减了一层for,下场就是,最后的近似值没有批梯度精确,不过够用了。
⑤迭代问题
如何确定迭代的次数?我们大可以设个500,让它算!但这不智能!
迭代停止条件目前分为两个。设精度是0.001
一、近似达到目标函数的极值,即变化小于0.001
二、各个参数Θi的变化小于0.001
一般达到这两个条件,就算是迭代比较完美了,再算其实意义不大。
标签:
原文地址:http://www.cnblogs.com/neopenx/p/4295543.html