标签:
题意:在n*m的矩阵中,有些格子有树,没有树的格子不能到达,找一条或多条回路,吃全然部的树,求有多少中方法。
这题是插头dp,刚刚学习,不是非常熟悉,研究了好几天才明确插头dp的方法,他们老是讲一些什么轮廓线啊,插头啊什么的,刚開始全然不知道这些事干什么的,看完cdq的大作后也是一头的雾水,看代码,绘图,一步一步的推,最终明确了,那个是为什么,这里讲一讲。
轮廓线表示的是当前插头的状态,这题中状态中1表示有插头,0表示无插头,假设是横线的话就是上面的格子与以下的格子相连的状态,这题中显然一个格子中要码有两个插头(经过这个格子),要码没有插头(不经过这个格子),由于不可能分叉走,每一个格子走一次。

这个状态表示(101111),当前决策格子是第二行第三个格子,显然它已经有了两个插头,也就是有1条线穿过它,所以不用再加插头了。
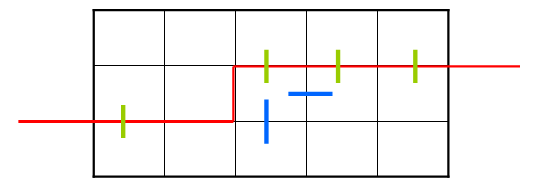

这个状态是(100111)和(101011),当前决策格子是第二行第三个格子,显然有一个插头了,再加入一个就可以,那么就有两个选择,要码向下,要码向右,就要有两个转移。
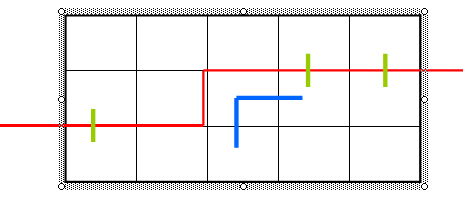
这个状态是(100011),当前决策格子是第二行第三个格子,显然之前没有有一个插头了,仅仅能加入两个,或者不加入,不加入,就肯定不经过这个格子,显然仅仅能这个格子是不可行的。
你自己推理一下,为什么要从i,j-1个格子中状态转移过来和上一层的状态转移到下层,你会发现轮廓线的美妙。
自己用笔画画吧,好记性不如烂笔头。
我參考的代码是 http://hi.baidu.com/fqq11679/blog/item/423bcd4a3d956bf983025c6d.html
只是状态转移上有点差别,他是当前状态转到后来状态,我是当前状态从前面转来。
//hdu1693 by huicpc0207
#include<iostream>
#include<stdio.h>
#include<string.h>
using namespace std;
const int N=13;
const int M=(1<<N);
typedef long long LL;
LL dp[N][N][M];
int n,m,g[N][N],cas;
void read()
{
scanf("%d%d",&n,&m);
for(int i=1;i<=n;i++)
for(int j=1;j<=m;j++)
scanf("%d",&g[i][j]);
}
void solve()
{
read();
memset(dp,0,sizeof dp);
dp[0][m][0]=1;
for(int i=1;i<=n;i++)
{
for(int k=0;k<(1<<m);++k)
dp[i][0][k<<1]=dp[i-1][m][k];
for(int j=1;j<=m;j++)
for(int k=0;k<(1<<m+1);k++)
{
int x=1<<j-1;
int y=1<<j;
if(g[i][j]==0)
{
if((k&x)==0&&(k&y)==0) dp[i][j][k]=dp[i][j-1][k];
else dp[i][j][k]=0;
}
else{
if((k&x)!=0&&(k&y)!=0)
dp[i][j][k]=dp[i][j-1][k^x^y];
else if((k&x)==0&&(k&y)==0)
dp[i][j][k]=dp[i][j-1][k^x^y];
else
dp[i][j][k]=dp[i][j-1][k]+dp[i][j-1][k^x^y];
}
// printf()
}
}
printf("Case %d: There are %I64d ways to eat the trees.\n",++cas,dp[n][m][0]);
}
int main()
{
// freopen("1.in","r",stdin);
int t; cas=0;
scanf("%d",&t);
while(t--) solve();
return 0;
}
标签:
原文地址:http://www.cnblogs.com/gcczhongduan/p/4296469.html