标签:
假期就这么结束了,不甘心啊!放假前还打算利用这段时间看看高数,学学微积分,想想如何实现精确的三体模拟.结果整个假期里,书都没有翻一下.罢了,发布下我写的使用势能守衡对三体进行近似模拟的代码,希望能够抛砖引玉.欢迎大家进来讨论,修改,优化.
空间中三个星体,在万有引力作用下的运动被称为三体运动.它的输入数据是:三个物体的质量,位置和速度.在万有引力的作用下,三个物体的位置和速度会时时发生变化.需要计算的是它们在某一时刻的位置与速度.
代码是C++的,首先要定义一个星体的结构体,包含星体的质量,位置和速度.还有一个"半径缩放"它与星体的质量有关,只是表示星体的体积,用于图形的渲染.
struct Body { Vec3 vPosition; // 位置 Vec3 vVelocity; // 速度 float fWeight; // 重量 float fRadiusScale; // 半径缩放 Body() { fWeight = 0.0f; fRadiusScale = 0.0f; } // 计算动能 float CalculateKineticEnergy() const { float sqv = vVelocity.MagnitudeSquared(); return 0.5f*fWeight*sqv; } // 设置动能,即通过动能计算速度 void SetKineticEnergy(float energy) { float v = sqrt(2*energy/fWeight); float w = vVelocity.Magnitude(); if (w < FLT_EPSILON) { vVelocity.x = v; } else { vVelocity *= v/w; } } // 设置质量 void SetWeight(float weight) { fWeight = weight; fRadiusScale = powf(weight, 1.0f/3.0f); } };
然后是定义一个三体世界的基类,这是一个抽象接口类.它包含三个星体对象和一个引力系数.如果你有自己的算法,可以继承该类实现它.
1 class IThreeBody 2 { 3 public: 4 5 IThreeBody() 6 { 7 m_fGravitationCoefficient = 100.0f; 8 } 9 10 // 重置 11 virtual void Reset() 12 { 13 RandomBody(m_bodyA); 14 RandomBody(m_bodyB); 15 RandomBody(m_bodyC); 16 } 17 18 // 按时更新 19 virtual void Update(float deltaTime) = NULL; 20 21 // 引力系数 22 virtual void SetGravitationCoefficient(float c) 23 { 24 m_fGravitationCoefficient = c; 25 } 26 27 // 星体A的重量 28 virtual void SetBodyAWeight(float weight) 29 { 30 m_bodyA.SetWeight(weight); 31 } 32 33 // 星体B的重量 34 virtual void SetBodyBWeight(float weight) 35 { 36 m_bodyB.SetWeight(weight); 37 } 38 39 // 星体C的重量 40 virtual void SetBodyCWeight(float weight) 41 { 42 m_bodyC.SetWeight(weight); 43 } 44 45 float GetGravitationCoefficient() const 46 { 47 return m_fGravitationCoefficient; 48 } 49 50 const Body& GetBodyA() const 51 { 52 return m_bodyA; 53 } 54 55 const Body& GetBodyB() const 56 { 57 return m_bodyB; 58 } 59 60 const Body& GetBodyC() const 61 { 62 return m_bodyC; 63 } 64 65 protected: 66 67 // 重置星体 68 void RandomBody(Body& body) 69 { 70 body.vPosition.x = rand2(-YD_THREE_BODY_EXTEND, YD_THREE_BODY_EXTEND); 71 body.vPosition.y = rand2(-YD_THREE_BODY_EXTEND, YD_THREE_BODY_EXTEND); 72 body.vPosition.z = rand2(-YD_THREE_BODY_EXTEND, YD_THREE_BODY_EXTEND); 73 74 body.vVelocity.x = rand2(-1, 1); 75 body.vVelocity.y = rand2(-1, 1); 76 body.vVelocity.z = rand2(-1, 1); 77 body.vVelocity.Normalize(); 78 body.vVelocity *= rand2(YD_THREE_BODY_VELOCITY*0.1f, YD_THREE_BODY_VELOCITY*0.5f); 79 80 body.fWeight = rand2(1.0f, 8.0f); 81 body.fRadiusScale = powf(body.fWeight, 1.0f/3.0f); 82 } 83 84 // 计算某一星体的加速度 85 void CalculateBodyAcceleration(const Body& body, const Body& s1, const Body& s2, Vec3& acc) 86 { 87 Vec3 v1 = s1.vPosition - body.vPosition; 88 float sqd1 = v1.MagnitudeSquared(); 89 if (sqd1 < YD_ESP) 90 { 91 sqd1 = YD_ESP; 92 } 93 float d1 = sqrt(sqd1); 94 float a1 = m_fGravitationCoefficient*s1.fWeight/sqd1; 95 96 Vec3 v2 = s2.vPosition - body.vPosition; 97 float sqd2 = v2.MagnitudeSquared(); 98 if (sqd2 < YD_ESP) 99 { 100 sqd2 = YD_ESP; 101 } 102 float d2 = sqrt(sqd2); 103 float a2 = m_fGravitationCoefficient*s2.fWeight/sqd2; 104 105 float a1x = a1*v1.x/d1; 106 float a1y = a1*v1.y/d1; 107 float a1z = a1*v1.z/d1; 108 109 float a2x = a2*v2.x/d2; 110 float a2y = a2*v2.y/d2; 111 float a2z = a2*v2.z/d2; 112 113 acc.x = a1x + a2x; 114 acc.y = a1y + a2y; 115 acc.z = a1z + a2z; 116 } 117 118 protected: 119 float m_fGravitationCoefficient; // 引力系数 120 121 Body m_bodyA; 122 Body m_bodyB; 123 Body m_bodyC; 124 };
接下来就是使用动能势能守衡对三体进行近似模拟的代码,即我实现的三体模拟,定义一个类MyThreeBody它是IThreeBody的子类:
1 class MyThreeBody : public IThreeBody 2 { 3 public: 4 MyThreeBody() 5 { 6 m_fPotentialEnergyAB = 0.0f; 7 m_fPotentialEnergyBC = 0.0f; 8 m_fPotentialEnergyAC = 0.0f; 9 m_fAmountOfEnergy = 0.0f; 10 } 11 12 // 重置 13 void Reset(); 14 15 // 按时更新 16 void Update(float deltaTime); 17 18 // 引力系数 19 void SetGravitationCoefficient(float c); 20 21 // 星体A的重量 22 void SetBodyAWeight(float weight); 23 24 // 星体B的重量 25 void SetBodyBWeight(float weight); 26 27 // 星体C的重量 28 void SetBodyCWeight(float weight); 29 30 protected: 31 32 // 更新星体的位置,速度 33 void UpdateBody(Body& body, float t, const Vec3& acc) 34 { 35 body.vPosition.x = body.vPosition.x + body.vVelocity.x*t + 0.5f*acc.x*t*t; 36 body.vPosition.y = body.vPosition.y + body.vVelocity.y*t + 0.5f*acc.y*t*t; 37 body.vPosition.z = body.vPosition.z + body.vVelocity.z*t + 0.5f*acc.z*t*t; 38 39 body.vVelocity.x += acc.x*t; 40 body.vVelocity.y += acc.y*t; 41 body.vVelocity.z += acc.z*t; 42 } 43 44 // 计算势能 45 void CalculatePotentialEnergy() 46 { 47 Vec3 vAB = m_bodyA.vPosition - m_bodyB.vPosition; 48 float disAB = vAB.Magnitude(); 49 if (disAB < YD_ESP) 50 { 51 disAB = YD_ESP; 52 } 53 m_fPotentialEnergyAB = -m_fGravitationCoefficient*m_bodyA.fWeight*m_bodyB.fWeight/disAB; 54 55 Vec3 vBC = m_bodyC.vPosition - m_bodyB.vPosition; 56 float disBC = vBC.Magnitude(); 57 if (disBC < YD_ESP) 58 { 59 disBC = YD_ESP; 60 } 61 m_fPotentialEnergyBC = -m_fGravitationCoefficient*m_bodyC.fWeight*m_bodyB.fWeight/disBC; 62 63 Vec3 vAC = m_bodyA.vPosition - m_bodyC.vPosition; 64 float disAC = vAC.Magnitude(); 65 if (disAC < YD_ESP) 66 { 67 disAC = YD_ESP; 68 } 69 m_fPotentialEnergyAC = -m_fGravitationCoefficient*m_bodyA.fWeight*m_bodyC.fWeight/disAC; 70 } 71 72 // 计算总能量 73 void CalculateAmountOfEnergy() 74 { 75 // 动能 76 float fKineticEnergyA = m_bodyA.CalculateKineticEnergy(); 77 float fKineticEnergyB = m_bodyB.CalculateKineticEnergy(); 78 float fKineticEnergyC = m_bodyC.CalculateKineticEnergy(); 79 80 // 势能 81 CalculatePotentialEnergy(); 82 83 // 总能量 84 m_fAmountOfEnergy = (m_fPotentialEnergyAB + m_fPotentialEnergyAC + m_fPotentialEnergyBC) + 85 fKineticEnergyA + fKineticEnergyB + fKineticEnergyC; 86 } 87 88 private: 89 float m_fPotentialEnergyAB; // 势能AB 90 float m_fPotentialEnergyBC; // 势能BC 91 float m_fPotentialEnergyAC; // 势能AC 92 float m_fAmountOfEnergy; // 三体总能量 93 };
MyThreeBody需要实现一个关键的函数Update(float deltaTime),它用于对三体的更新,输入一个间隔时间,计算出当前三个物体的位置与速度:
1 void MyThreeBody::Update(float deltaTime) 2 { 3 Vec3 accA, accB, accC; 4 CalculateBodyAcceleration(m_bodyA, m_bodyB, m_bodyC, accA); 5 CalculateBodyAcceleration(m_bodyB, m_bodyC, m_bodyA, accB); 6 CalculateBodyAcceleration(m_bodyC, m_bodyA, m_bodyB, accC); 7 8 UpdateBody(m_bodyA, deltaTime, accA); 9 UpdateBody(m_bodyB, deltaTime, accB); 10 UpdateBody(m_bodyC, deltaTime, accC); 11 12 // 动能 13 float fKineticEnergyA = m_bodyA.CalculateKineticEnergy(); 14 float fKineticEnergyB = m_bodyB.CalculateKineticEnergy(); 15 float fKineticEnergyC = m_bodyC.CalculateKineticEnergy(); 16 17 // 势能 18 CalculatePotentialEnergy(); 19 20 // 能量守恒 21 float fKineticEnergy = m_fAmountOfEnergy - (m_fPotentialEnergyAB + m_fPotentialEnergyAC + m_fPotentialEnergyBC); 22 if (fKineticEnergy < 0.0f) 23 { 24 fKineticEnergy = 0.0f; 25 } 26 27 float fKineticEnergy2 = fKineticEnergyA + fKineticEnergyB + fKineticEnergyC; 28 float r = fKineticEnergy/fKineticEnergy2; 29 if (r > YD_ESP) 30 { 31 fKineticEnergyA *= r; 32 fKineticEnergyB *= r; 33 fKineticEnergyC *= r; 34 } 35 else 36 { 37 fKineticEnergyA = 1.0f; 38 fKineticEnergyB = 1.0f; 39 fKineticEnergyC = 1.0f; 40 } 41 42 m_bodyA.SetKineticEnergy(fKineticEnergyA); 43 m_bodyB.SetKineticEnergy(fKineticEnergyB); 44 m_bodyC.SetKineticEnergy(fKineticEnergyC); 45 }
这里使用了两个物理定律:
(1)万有引力定律
这是牛顿发现的:任意两个质点有通过连心线方向上的力相互吸引。该引力的大小与它们的质量乘积成正比,与它们距离的平方成反比,与两物体的化学本质或物理状态以及中介物质无关。
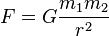
其中:
依照国际单位制,F的单位为牛顿(N),m1和m2的单位为千克(kg),r 的单位为米(m),常数G近似地等于6.67 × 10−11 N m2 kg−2(牛顿米的平方每千克的平方)。当然程序中G不可能设置为这么小的一个数,用户可以自己设置万有引力常数,以实现合理的运动.
(2)势能与动能守恒定律
引力位能或引力势能是指物体因为大质量物体的万有引力而具有的位能,其大小与其到大质量的距离有关。
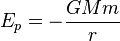
其中:
动能,简单的说就是指物体因运动而具有的能量。数值上等于(1/2)Mv^2. 动能是能量的一种,它的国际单位制下单位是焦耳(J),简称焦。
势能与动能守恒即在整个运动过程中,其总能量是不变的,即三体的动能与势能之和为固定值.
若想要对三体进行精确的模拟必需使用微积分,希望有人能继续下去.
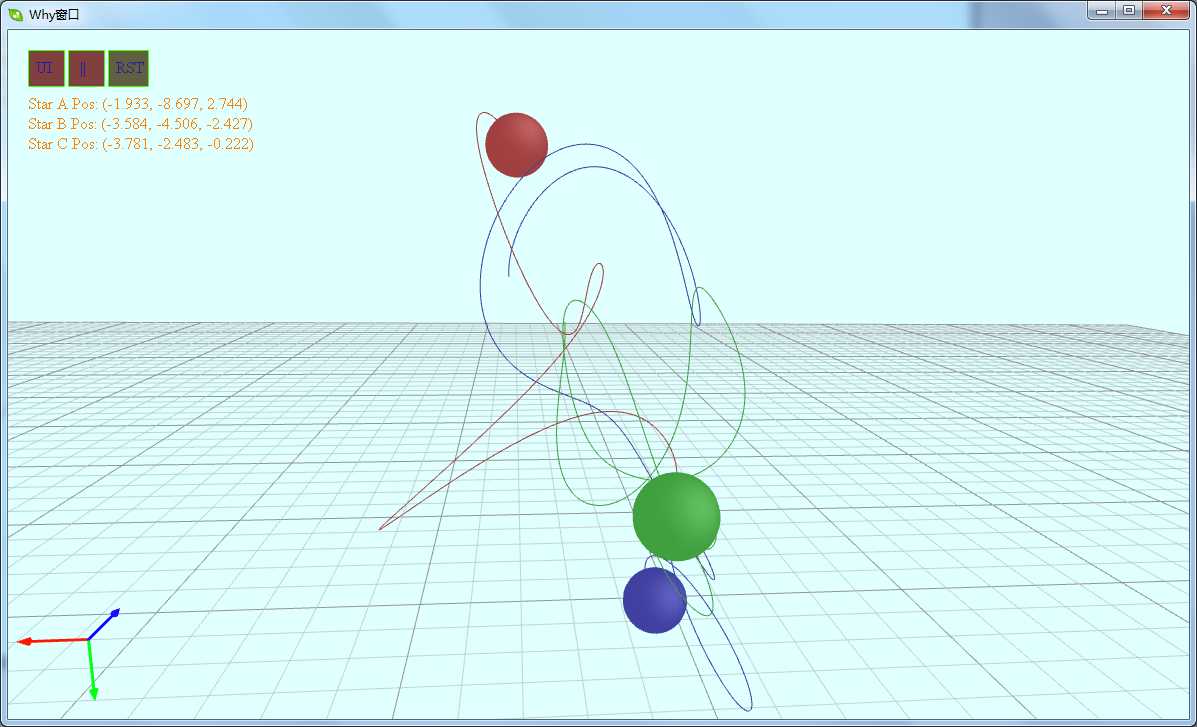
下载地址:
http://files.cnblogs.com/files/WhyEngine/SanTi.7z
代码开发环境是VS2008.并提供了debug和release两套测试环境.
如果你打算自己编译下该工程,还需要下载WHY引擎的库文件:
http://files.cnblogs.com/files/WhyEngine/WhyLib.7z
如果你对代码做出了修改,将编译出的"SanTi.dll"替换下原有的"SanTi.dll"即可测试.
相关文章:
标签:
原文地址:http://www.cnblogs.com/WhyEngine/p/4299422.html