标签:
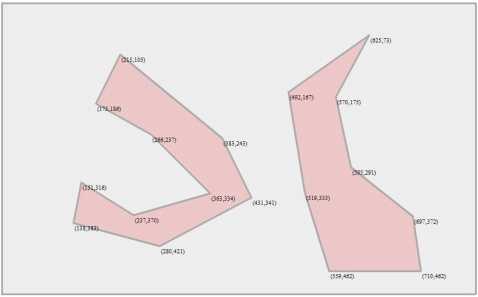
假设上图是一个游戏地图,红色的区域是不可行走的区域,浅灰色区域是可行走区域,要想在游戏中实现nav寻路,必须将可行走区域转化为nav网格并保存为一种固定形式的数据,如下图浅红色的三角形。
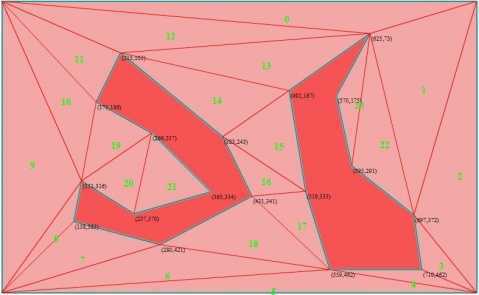
nav网格必须是凸多边形,这里使用三角型,当然也可以使用4边形。下面介绍一种任意多边形的三角化算法。算法来自论文《平面多边形域的快速约束 三角化》作者:曾薇 孟祥旭 杨承磊 杨义军。详细内容请参考该论文。
先来看几个定义:
A. 我们称点 p3 为直线 p1p2 的可见点,其必须满足下面三个条件:
(1) p3 在边 p1p2 的右侧 (顶点顺序为顺时针);
(2) p3 与 p1 可见,即 p1p3 不与任何一个约束边相交;
(3) p3 与 p2 可见
B. DT点
在一个约束Delaunay三角形中,其中与一条边相对的顶点称为该边的DT点。
确定 DT 点的过程如下:
Step1. 构造 Δp1p2p3 的外接圆 C(p1,p2,p3)及其网格包围盒 B(C(p1,p2,p3))
Step2. 依次访问网格包围盒内的每个网格单元:
对未作当前趟数标记的网格单元进行搜索,并将其标记为当前趟数
若某个网格单元中存在可见点 p, 并且 ∠p1pp2 > ∠p1p3p2,则令 p3=p1,转Step1;否则,转Step3.
Step3. 若当前网格包围盒内所有网格单元都已被标记为当前趟数,也即C(p1,p2,p3)内无可见点,则 p3 为的 p1p2 的 DT 点
生成Delaunay三角网格算法如下:
Step2. 取任意一条外边界边 p1p2 .
Step3. 计算 DT 点 p3,构成约束 Delaunay 三角形 Δp1p2p3 .
Step4. 如果新生成的边 p1p3 不是约束边,若已经在堆栈中,则将其从中删除;否则,将其放入堆栈;类似地,可处理 p3p2 .
Step5. 若堆栈不空,则从中取出一条边,转Step3;否则,算法停止 .
程序实现该算法(AS3语言)
1。数据结构
不难看出,要想实现该算法首先要确定一些基础对象,如点、线、三角型和多边形等对象。(才发现这个blog中竟然没有代码的格式 )
)
二维点的定义 public class Vector2f {} 包括矢量加减、叉积等方法。
线的定义 public class Line2D {} 包括下面方法:
classifyPoint(point:Vector2f, epsilon:Number = 0.000001):int //判断点与直线的关系,假设你站在a点朝向b点, 则输入点与直线的关系分为:Left, Right or Centered on the line equals(line:Line2D):Boolean //线段是否相等 (忽略方向) getDirection():Vector2f //直线方向 intersection(other:Line2D, pIntersectPoint:Vector2f = null):int //判断两个直线关系 this line A = x0, y0 and B = x1, y1 other is A = x2, y2 and B = x3, y3 length():Number //直线长度 signedDistance(point:Vector2f):Number //给定点到直线的带符号距离,从a点朝向b点,右向为正,左向为负
三角型定义 public class Triangle:
getSide(sideIndex:int):Line2D //取得指定索引的边(从0开始,顺时针) getVertex(i:int):Vector2f //根据i返回顶点 isPointIn(testPoint:Vector2f):Boolean //测试给定点是否在三角型中 setVertex(i:int, point:Vector2f):void //根据i指定的索引设置三角形的顶点
多边形定义 public class Polygon:
public vertexV : Vector.<Vector2f> //顶点列表,按顺时针方向排序 cw():void //将多边形的顶点按逆时针排序 isCW():Boolean //将多边形的顶点按顺时针排序 isSimplicity():Boolean //是否是简单多边形 rectangle():Rectangle //返回矩形包围盒 Polygon union(polygon:Polygon):Vector.<Polygon> //合并两个多边形(Weiler-Athenton算法)
三角化的完整代码,注释比较全,就不再详细解释了
/* * @author 白连忱 * date Jan 22, 2010 */ package org.blch.geom { import flash.display.Sprite; import flash.geom.Rectangle; import flash.text.TextField; import flash.text.TextFieldAutoSize; import flash.text.TextFormat; /** * Delaunay * @langversion ActionScript 3.0 * @playerversion Flash 10.0 */ public class Delaunay { public function Delaunay() { } private static const EPSILON:Number = 0.000001; //精度 private var polygonV:Vector.<Polygon>; //所有多边形,第0个元素为区域外边界 (输入数据) private var vertexV:Vector.<Vector2f>; //所有顶点列表, 前outEdgeVecNmu个为外边界顶点 private var edgeV:Vector.<Line2D>; //所有约束边 private var outEdgeVecNmu:int; //区域外边界顶点数 private var lineV:Vector.<Line2D>; //线段堆栈 private var triangleV:Vector.<Triangle>; //生成的Delaunay三角形 public function createDelaunay(polyV:Vector.<Polygon>):Vector.<Triangle> { //Step1. 建立单元大小为 E*E 的均匀网格,并将多边形的顶点和边放入其中. // 其中 E=sqrt(w*h/n),w 和 h 分别为多边形域包围盒的宽度、高度,n 为多边形域的顶点数 . initData(polyV); //Step2. 取任意一条外边界边 p1p2 . var initEdge:Line2D = getInitOutEdge(); lineV.push(initEdge); var edge:Line2D; do { //Step3. 计算 DT 点 p3,构成约束 Delaunay 三角形 Δp1p2p3 . edge = lineV.pop(); // trace("开始处理edge###########:", edge); var p3:Vector2f = findDT(edge); if (p3 == null) continue; var line13:Line2D = new Line2D(edge.getPointA(), p3); var line32:Line2D = new Line2D(p3, edge.getPointB()); //Delaunay三角形放入输出数组 var trg:Triangle = new Triangle(edge.getPointA(), edge.getPointB(), p3); // trace("DT 点p3", p3); // trace("Triangle", trg); triangleV.push(trg); //Step4. 如果新生成的边 p1p3 不是约束边,若已经在堆栈中, // 则将其从中删除;否则,将其放入堆栈;类似地,可处理 p3p2 . var index:int; if (indexOfVector(line13, this.edgeV) < 0) { index = indexOfVector(line13, lineV); if (index > -1) { lineV.splice(index, 1); } else { lineV.push(line13); } } if (indexOfVector(line32, this.edgeV) < 0) { index = indexOfVector(line32, lineV); if (index > -1) { lineV.splice(index, 1); } else { lineV.push(line32); } } //Step5. 若堆栈不空,则从中取出一条边,转Step3;否则,算法停止 . // trace("处理结束edge###########\n"); } while (lineV.length > 0); return triangleV; } /** * 初始化数据 * @param polyV */ private function initData(polyV:Vector.<Polygon>):void { //填充顶点和线列表 vertexV = new Vector.<Vector2f>(); edgeV = new Vector.<Line2D>(); var poly:Polygon; for (var i:int=0; i<polyV.length; i++) { poly = polyV[i]; putVertex(vertexV, poly.vertexV); putEdge(edgeV, poly.vertexV); } outEdgeVecNmu = polyV[0].vertexNmu; lineV = new Vector.<Line2D>(); triangleV = new Vector.<Triangle>(); } /** * 获取初始外边界 * @return */ private function getInitOutEdge():Line2D { var initEdge:Line2D = edgeV[0]; //检查是否有顶点p在该边上,如果有则换一个外边界 var loopSign:Boolean; var loopIdx:int = 0; do { loopSign = false; loopIdx++; for each (var testV:Vector2f in this.vertexV) { if ( testV.equals(initEdge.getPointA()) || testV.equals(initEdge.getPointB()) ) continue; if (initEdge.classifyPoint(testV, EPSILON) == PointClassification.ON_LINE) { loopSign = true; initEdge = edgeV[loopIdx]; break; } } } while (loopSign && loopIdx<outEdgeVecNmu-1); //只取外边界 return initEdge; } /** * 将srcV中的点放入dstV * @param dstV * @param srcV */ private function putVertex(dstV:Vector.<Vector2f>, srcV:Vector.<Vector2f>):void { for each (var item:Vector2f in srcV) { dstV.push(item); } } /** * 根据srcV中的点生成多边形线段,并放入dstV * @param dstV * @param srcV */ private function putEdge(dstV:Vector.<Line2D>, srcV:Vector.<Vector2f>):void { if (srcV.length < 3) return; //不是一个多边形 var p1:Vector2f = srcV[0]; var p2:Vector2f; for (var i:int=1; i<srcV.length; i++) { p2 = srcV[i]; dstV.push(new Line2D(p1, p2)); p1 = p2; } p2 = srcV[0]; dstV.push(new Line2D(p1, p2)); } /** * 判断线段是否是约束边 * @param line * @return 线段的索引,如果没有找到,返回-1 */ private function indexOfVector(line:Line2D, vector:Vector.<Line2D>):int { var lt:Line2D; for (var i:int=0; i<vector.length; i++) { lt = vector[i]; if (lt.equals(line)) return i; } return -1; } /** * 计算 DT 点 * @param line * @return */ private function findDT(line:Line2D):Vector2f { var p1:Vector2f = line.getPointA(); var p2:Vector2f = line.getPointB(); //搜索所有可见点 TODO 按y方向搜索距线段终点最近的点 var allVPoint:Vector.<Vector2f> = new Vector.<Vector2f>(); // line的所有可见点 for each (var vt:Vector2f in this.vertexV) { if (isVisiblePointOfLine(vt, line)) { allVPoint.push(vt); } } if (allVPoint.length == 0) return null; var p3:Vector2f = allVPoint[0]; var loopSign:Boolean = false; do { loopSign = false; //Step1. 构造 Δp1p2p3 的外接圆 C(p1,p2,p3)及其网格包围盒 B(C(p1,p2,p3)) var circle:Circle = this.circumCircle(p1, p2, p3); var boundsBox:Rectangle = this.circleBounds(circle); //Step2. 依次访问网格包围盒内的每个网格单元: // 若某个网格单元中存在可见点 p, 并且 ∠p1pp2 > ∠p1p3p2,则令 p3=p,转Step1;否则,转Step3. var angle132:Number = Math.abs(lineAngle(p1, p3, p2)); // ∠p1p3p2 for each (var vec:Vector2f in allVPoint) { if ( vec.equals(p1) || vec.equals(p2) || vec.equals(p3) ) { continue; } //不在包围盒中 if (boundsBox.contains(vec.x, vec.y) == false) { continue; } //夹角 var a1:Number = Math.abs(lineAngle(p1, vec, p2)); if (a1 > angle132) { /////转Step1 p3 = vec; loopSign = true; break; } } ///////转Step3 } while (loopSign); //Step3. 若当前网格包围盒内所有网格单元都已被处理完, // 也即C(p1,p2,p3)内无可见点,则 p3 为的 p1p2 的 DT 点 return p3; } /** * 返回顶角在o点,起始边为os,终止边为oe的夹角, 即∠soe (单位:弧度) * 角度小于pi,返回正值; 角度大于pi,返回负值 */ private function lineAngle(s:Vector2f, o:Vector2f, e:Vector2f):Number { var cosfi:Number, fi:Number, norm:Number; var dsx:Number = s.x - o.x; var dsy:Number = s.y - o.y; var dex:Number = e.x - o.x; var dey:Number = e.y - o.y; cosfi = dsx*dex + dsy*dey; norm = (dsx*dsx + dsy*dsy) * (dex*dex + dey*dey); cosfi /= Math.sqrt( norm ); if (cosfi >= 1.0 ) return 0; if (cosfi <= -1.0 ) return -Math.PI; fi = Math.acos(cosfi); if (dsx*dey - dsy*dex > 0) return fi; // 说明矢量os 在矢量 oe的顺时针方向 return -fi; } /** * 返回圆的包围盒 * @param c * @return */ private function circleBounds(c:Circle):Rectangle { return new Rectangle(c.center.x-c.r, c.center.y-c.r, c.r*2, c.r*2); } /** * 返回三角形的外接圆 * @param p1 * @param p2 * @param p3 * @return */ private function circumCircle(p1:Vector2f, p2:Vector2f, p3:Vector2f):Circle { var m1:Number,m2:Number,mx1:Number,mx2:Number,my1:Number,my2:Number; var dx:Number,dy:Number,rsqr:Number,drsqr:Number; var xc:Number, yc:Number, r:Number; /* Check for coincident points */ if ( Math.abs(p1.y-p2.y) < EPSILON && Math.abs(p2.y-p3.y) < EPSILON ) { trace("CircumCircle: Points are coincident."); return null; } m1 = - (p2.x - p1.x) / (p2.y - p1.y); m2 = - (p3.x-p2.x) / (p3.y-p2.y); mx1 = (p1.x + p2.x) / 2.0; mx2 = (p2.x + p3.x) / 2.0; my1 = (p1.y + p2.y) / 2.0; my2 = (p2.y + p3.y) / 2.0; if ( Math.abs(p2.y-p1.y) < EPSILON ) { xc = (p2.x + p1.x) / 2.0; yc = m2 * (xc - mx2) + my2; } else if ( Math.abs(p3.y - p2.y) < EPSILON ) { xc = (p3.x + p2.x) / 2.0; yc = m1 * (xc - mx1) + my1; } else { xc = (m1 * mx1 - m2 * mx2 + my2 - my1) / (m1 - m2); yc = m1 * (xc - mx1) + my1; } dx = p2.x - xc; dy = p2.y - yc; rsqr = dx*dx + dy*dy; r = Math.sqrt(rsqr); return new Circle(new Vector2f(xc, yc), r); } /** * 判断点vec是否为line的可见点 * @param vec * @param line * @return true:vec是line的可见点 */ private function isVisiblePointOfLine(vec:Vector2f, line:Line2D):Boolean { if (vec.equals(line.getPointA()) || vec.equals(line.getPointB())) { return false; } //(1) p3 在边 p1p2 的右侧 (多边形顶点顺序为顺时针); if (line.classifyPoint(vec, EPSILON) != PointClassification.RIGHT_SIDE) { return false; } //(2) p3 与 p1 可见,即 p1p3 不与任何一个约束边相交; if (isVisibleIn2Point(line.getPointA(), vec) == false) { return false; } //(3) p3 与 p2 可见 if (isVisibleIn2Point(line.getPointB(), vec) == false) { return false; } return true; } /** * 点pa和pb是否可见(pa和pb构成的线段不与任何约束边相交,不包括顶点) * @param pa * @param pb * @return */ private function isVisibleIn2Point(pa:Vector2f, pb:Vector2f):Boolean { var linepapb:Line2D = new Line2D(pa, pb); var interscetVector:Vector2f = new Vector2f(); //线段交点 for each (var lineTmp:Line2D in this.edgeV) { //两线段相交 if (linepapb.intersection(lineTmp, interscetVector) == LineClassification.SEGMENTS_INTERSECT) { //交点是不是端点 if ( !pa.equals(interscetVector) && !pb.equals(interscetVector) ) { return false; } } } return true; } } } import org.blch.geom.Vector2f; /** * 圆 * @author blc */ class Circle { public var center:Vector2f; //圆心 public var r:Number; //半径 public function Circle(cen:Vector2f, r:Number) { this.center = cen; this.r = r; } }
标签:
原文地址:http://www.cnblogs.com/zdlbbg/p/4301307.html