标签:
如果你也实现了上一章提到的代码,不难发现对下图的两种情况会出现问题
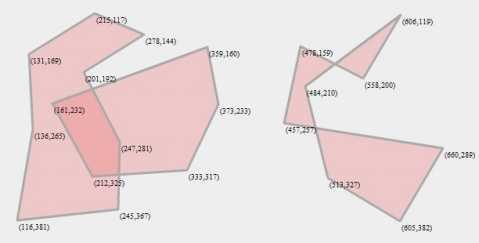
左面的是两个区域有相交的情况,右面的是多边形本身有自交,在这两种情况下,前面给出的代码均会产生错误的结果。
对于两个多边形相交,可以在生成网格之前先合并多边形,合并后如图
合并算法在前面多边形剪裁处已给出一个,这里只贴上代码:
/** * 合并两个多边形(Weiler-Athenton算法) * @param polygon * @return * null--两个多边形不相交,合并前后两个多边形不变 * Polygon--一个新的多边形 */ public function union(polygon:Polygon):Vector.<Polygon> { //包围盒不相交 if (rectangle().intersection(polygon.rectangle()) == false) { return null; } //所有顶点和交点 var cv0:Vector.<Node> = new Vector.<Node>();//主多边形 var cv1:Vector.<Node> = new Vector.<Node>();//合并多边形 //初始化 var node:Node; for (var i:int=0; i<this.vertexV.length; i++) { node = new Node(this.vertexV[i], false, true); if (i > 0) { cv0[i-1].next = node; } cv0.push(node); } for (var j:int=0; j<polygon.vertexV.length; j++) { node = new Node(polygon.vertexV[j], false, false); if (j > 0) { cv1[j-1].next = node; } cv1.push(node); } //插入交点 var insCnt:int = this.intersectPoint(cv0, cv1); //生成多边形 if (insCnt > 0) { //顺时针序 return linkToPolygon(cv0, cv1); } else { return null; } return null; } /** * 生成多边形,顺时针序; 生成的内部孔洞多边形为逆时针序 * @param cv0 * @param cv1 * @return 合并后的结果多边形数组(可能有多个多边形) */ private function linkToPolygon(cv0:Vector.<Node>, cv1:Vector.<Node>):Vector.<Polygon> { trace("linkToPolygon***linkToPolygon"); //保存合并后的多边形数组 var rtV:Vector.<Polygon> = new Vector.<Polygon>(); //1. 选取任一没有被跟踪过的交点为始点,将其输出到结果多边形顶点表中. for each (var testNode:Node in cv0) { if (testNode.i == true && testNode.p == false) { var rcNodes:Vector.<Vector2f> = new Vector.<Vector2f>(); while (testNode != null) { testNode.p = true; // 如果是交点 if (testNode.i == true) { testNode.other.p = true; if (testNode.o == false) { //该交点为进点(跟踪裁剪多边形边界) if (testNode.isMain == true) { //当前点在主多边形中 testNode = testNode.other; //切换到裁剪多边形中 } } else { //该交点为出点(跟踪主多边形边界) if (testNode.isMain == false) { //当前点在裁剪多边形中 testNode = testNode.other; //切换到主多边形中 } } } rcNodes.push(testNode.v); ////// 如果是多边形顶点,将其输出到结果多边形顶点表中 if (testNode.next == null) { //末尾点返回到开始点 if (testNode.isMain) { testNode = cv0[0]; } else { testNode = cv1[0]; } } else { testNode = testNode.next; } //与首点相同,生成一个多边形 if (testNode.v.equals(rcNodes[0])) break; } //提取 rtV.push(new Polygon(rcNodes.length, rcNodes)); } } trace("rtV", rtV); return rtV; } /** * 生成交点,并按顺时针序插入到顶点表中 * @param cv0 (in/out)主多边形顶点表,并返回插入交点后的顶点表 * @param cv1 (in/out)合并多边形顶点表,并返回插入交点后的顶点表 * @return 交点数 */ private function intersectPoint(cv0:Vector.<Node>, cv1:Vector.<Node>):int { var insCnt:int = 0; //交点数 var findEnd:Boolean = false; var startNode0:Node = cv0[0]; var startNode1:Node; var line0:Line2D; var line1:Line2D; var ins:Vector2f; var hasIns:Boolean; var result:int; //进出点判断结果 while (startNode0 != null) { //主多边形 if (startNode0.next == null) { //最后一个点,跟首点相连 line0 = new Line2D(startNode0.v, cv0[0].v); } else { line0 = new Line2D(startNode0.v, startNode0.next.v); } startNode1 = cv1[0]; hasIns = false; while (startNode1 != null) { //合并多边形 if (startNode1.next == null) { line1 = new Line2D(startNode1.v, cv1[0].v); } else { line1 = new Line2D(startNode1.v, startNode1.next.v); } ins = new Vector2f(); //接受返回的交点 //有交点 if (line0.intersection(line1, ins) == LineClassification.SEGMENTS_INTERSECT) { //忽略交点已在顶点列表中的 if (this.getNodeIndex(cv0, ins) == -1) { insCnt++; ///////// 插入交点 var node0:Node = new Node(ins, true, true); var node1:Node = new Node(ins, true, false); cv0.push(node0); cv1.push(node1); //双向引用 node0.other = node1; node1.other = node0; //插入 node0.next = startNode0.next; startNode0.next = node0; node1.next = startNode1.next; startNode1.next = node1; //出点 if (line0.classifyPoint(line1.getPointB()) == PointClassification.RIGHT_SIDE) { node0.o = true; node1.o = true; } //TODO 线段重合 // trace("交点****", node0); hasIns = true; //有交点 //有交点,返回重新处理 break; } } startNode1 = startNode1.next; } //如果没有交点继续处理下一个边,否则重新处理该点与插入的交点所形成的线段 if (hasIns == false) { startNode0 = startNode0.next; } } return insCnt; } /** * 取得节点的索引(合并多边形用) * @param cv * @param node * @return */ private function getNodeIndex(cv:Vector.<Node>, node:Vector2f):int { for (var i:int=0; i<cv.length; i++) { if (cv[i].v.equals(node)) { return i; } } return -1; } 对于一个给定的多边形数组polygonV,可以象下面这样在三角化以前做预处理 /** * 合并 */ private function unionAll():void { for (var n:int=1; n<polygonV.length; n++) { var p0:Polygon = polygonV[n]; for (var m:int=1; m<polygonV.length; m++) { var p1:Polygon = polygonV[m]; if (p0 != p1 && p0.isCW() && p1.isCW()) { var v:Vector.<Polygon> = p0.union(p1); //合并 if (v != null && v.length > 0) { trace("delete"); polygonV.splice(polygonV.indexOf(p0), 1); polygonV.splice(polygonV.indexOf(p1), 1); for each (var pv:Polygon in v) { polygonV.push(pv); } n = 1; //重新开始 break; } } } } }
对于多边形自交,可以采用类似多边形剪裁的方法将一个多边形拆分成多个,也可以直接禁止用户绘制这种多边形。我是采用后一种方法所以这里没有代码。
多边形的顶点顺序,上面多处代码都要求多边形顶点按顺时针或逆时针方向保存,但是我们不可能要求用户按哪个固定方向绘制图形,那么怎么判断多边形的顶点顺序。方法的基本思路就是取一个多边形的凸点,然后判断这个点的下一个点的方向,代码如下:
/** * 将多边形的顶点按顺时针排序 */ public function cw():void { if (this.isCW() == false) { //如果为逆时针顺序, 反转为顺时针 this.vertexV.reverse(); //反转数组 } } /** * clockwise * @return true -- clockwise; false -- counter-clockwise */ public function isCW():Boolean { if (vertexV == null || vertexV.length < 0) return false; //最上(y最小)最左(x最小)点, 肯定是一个凸点 //寻找最上点 var topPt:Vector2f = this.vertexV[0]; var topPtId:int = 0; //点的索引 for (var i:int=1; i<vertexV.length; i++) { if (topPt.y > vertexV[i].y) { topPt = vertexV[i]; topPtId = i; } else if (topPt.y == vertexV[i].y) { //y相等时取x最小 if (topPt.x > vertexV[i].x) { topPt = vertexV[i]; topPtId = i; } } } //凸点的邻点 var lastId:int = topPtId-1>=0 ? topPtId-1 : vertexV.length-1; var nextId:int = topPtId+1>=vertexV.length ? 0 : topPtId+1; var last:Vector2f = vertexV[lastId]; var next:Vector2f = vertexV[nextId]; //判断 var r:Number = multiply(last, next, topPt); if (r < 0) { return true; //三点共线情况不存在,若三点共线则说明必有一点的y(斜线)或x(水平线)小于topPt } return false; } /** * r=multiply(sp,ep,op),得到(sp-op)*(ep-op)的叉积 * r>0:ep在矢量opsp的逆时针方向; * r=0:opspep三点共线; * r<0:ep在矢量opsp的顺时针方向 * @param sp * @param ep * @param op * @return */ private function multiply(sp:Vector2f, ep:Vector2f, op:Vector2f):Number { return((sp.x-op.x)*(ep.y-op.y)-(ep.x-op.x)*(sp.y-op.y)); }
到此生成网格的关键代码都发出来了,下一章放上寻路的代码
标签:
原文地址:http://www.cnblogs.com/zdlbbg/p/4301320.html