标签:
原文链接:caffe.berkeleyvision.org/tutorial/layers.html
创建caffe模型,首先要在protocol buffer 定义文件(prototxt)中定义结构。
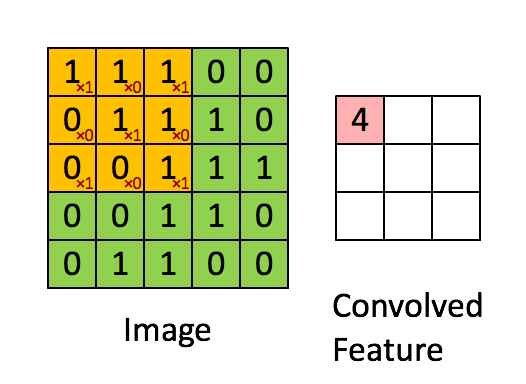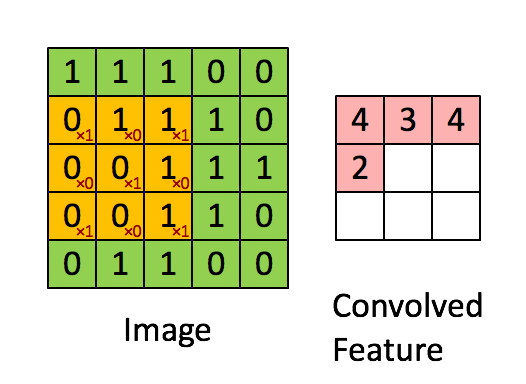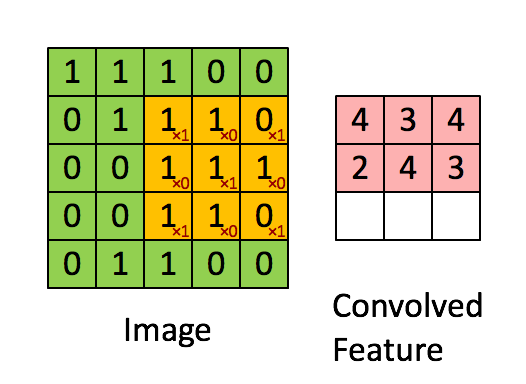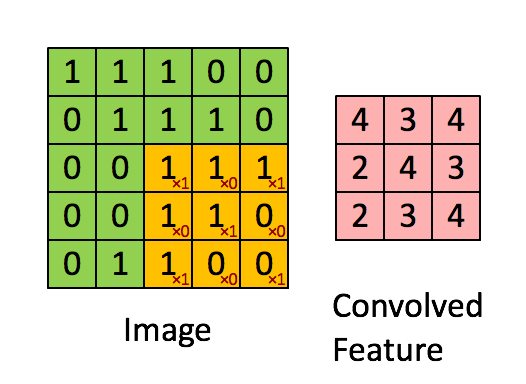
在caffe环境中,图像的明显特征是其空间结构。
Documents:
1 Parameters (ConvolutionParameter convolution_param) 2 3 Required 4 num_output (c_o): 输出数(filter数) 5 kernel_size (or kernel_h and kernel_w): 指定卷积核 6 7 Strongly Recommended 8 weight_filler [default type: ‘constant‘ value: 0] 9 10 Optional 11 bias_term [default true]: 指定是否提供偏置10 12 pad (or pad_h and pad_w) [default 0]: 指定输入图片的两侧像素填充量 13 stride (or stride_h and stride_w) [default 1]: specifies the intervals at which to apply the filters to the input 14 group (g) [default 1]: 如果 g > 1, 我们限制每一个filter之间的连通性 对于输入的子集. 指定输入和输出被分为 g 组,第i输出组只会和第i输入组相连接. 15 16 Input 17 18 n * c_i * h_i * w_i 19 20 Output 21 22 n * c_o * h_o * w_o, where h_o = (h_i + 2 * pad_h - kernel_h) / stride_h + 1 and w_o likewise.
example:
1 layers { 2 name: "conv1" 3 type: CONVOLUTION 4 bottom: "data" 5 top: "conv1" 6 blobs_lr: 1 # learning rate multiplier for the filters 7 blobs_lr: 2 # learning rate multiplier for the biases 8 weight_decay: 1 # weight decay multiplier for the filters 9 weight_decay: 0 # weight decay multiplier for the biases 10 convolution_param { 11 num_output: 96 # learn 96 filters 12 kernel_size: 11 # each filter is 11x11 13 stride: 4 # step 4 pixels between each filter application 14 weight_filler { 15 type: "gaussian" # initialize the filters from a Gaussian 16 std: 0.01 # distribution with stdev 0.01 (default mean: 0) 17 } 18 bias_filler { 19 type: "constant" # initialize the biases to zero (0) 20 value: 0 21 } 22 } 23 }
Pooling:
deeplearning.stanford.edu/wiki/index.php/池化
池化: 概述
在通过卷积获得了特征 (features) 之后,下一步我们希望利用这些特征去做分类。理论上讲,人们可以用所有提取得到的特征去训练分类器,例如 softmax 分类器,但这样做面临计算量的挑战。例如:对于一个 96X96 像素的图像,假设我们已经学习得到了400个定义在8X8输入上的特征,每一个特征和图像卷积都会得到一个 (96 − 8 + 1) * (96 − 8 + 1) = 7921 维的卷积特征,由于有 400 个特征,所以每个样例 (example) 都会得到一个 892 * 400 = 3,168,400 维的卷积特征向量。学习一个拥有超过 3 百万特征输入的分类器十分不便,并且容易出现过拟合 (over-fitting)。
为了解决这个问题,首先回忆一下,我们之所以决定使用卷积后的特征是因为图像具有一种“静态性”的属性,这也就意味着在一个图像区域有用的特征极有可能在 另一个区域同样适用。因此,为了描述大的图像,一个很自然的想法就是对不同位置的特征进行聚合统计,例如,人们可以计算图像一个区域上的某个特定特征的平 均值 (或最大值)。这些概要统计特征不仅具有低得多的维度 (相比使用所有提取得到的特征),同时还会改善结果(不容易过拟合)。这种聚合的操作就叫做池化 (pooling),有时也称为平均池化或者最大池化 (取决于计算池化的方法)。
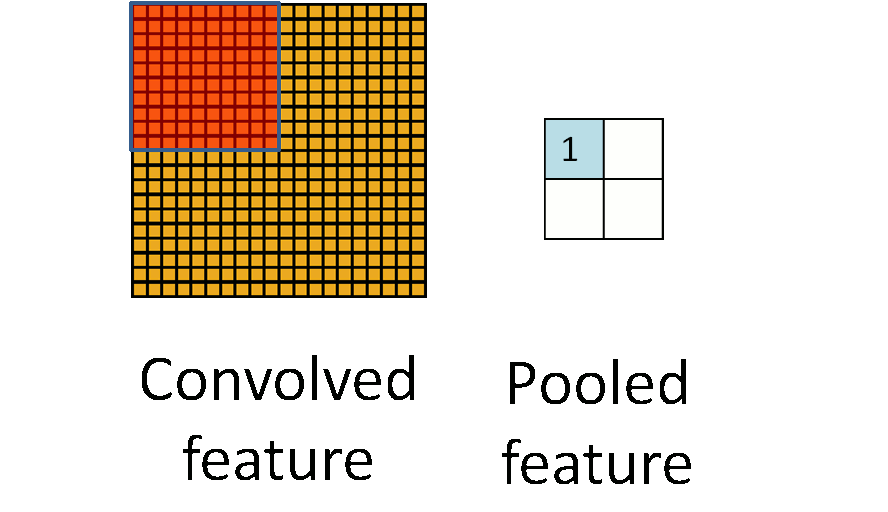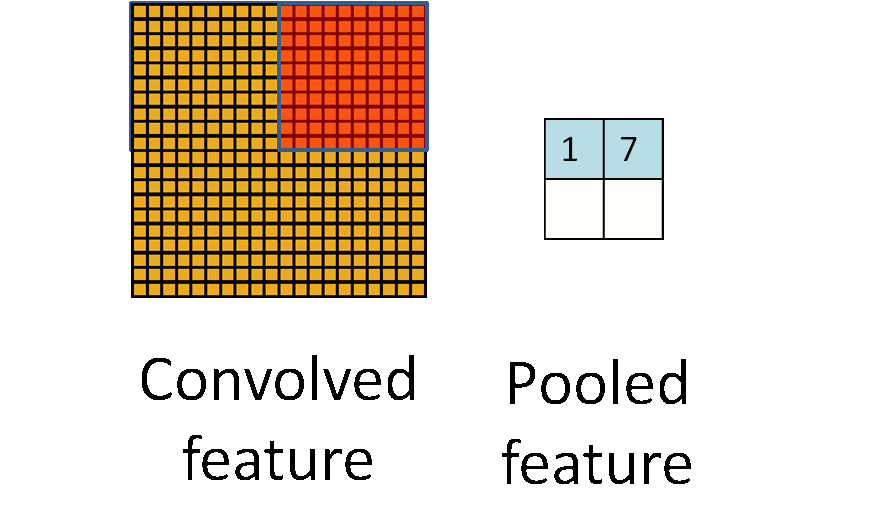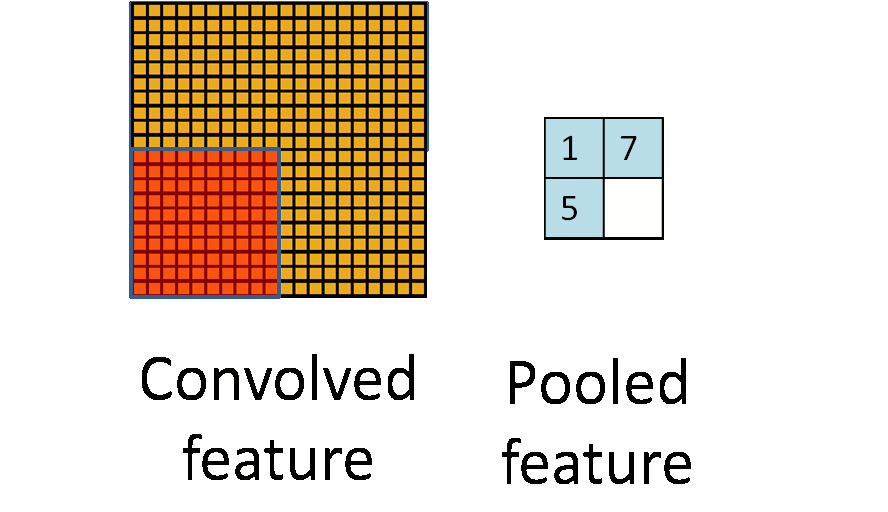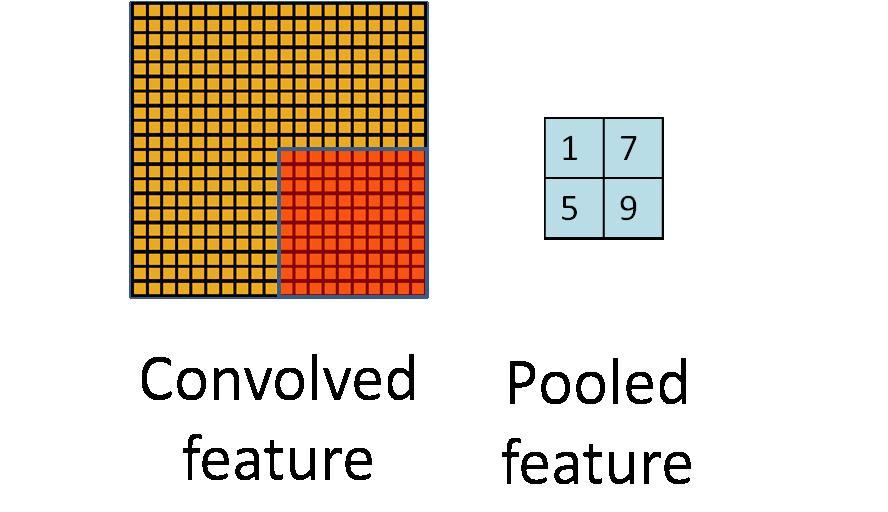
标签:
原文地址:http://www.cnblogs.com/nwpuxuezha/p/4302024.html