标签:
KMeans算法的基本思想是初始随机给定K个簇中心,按照最邻近原则把待分类样本点分到各个簇。然后按平均法重新计算各个簇的质心,从而确定新的簇心。一直迭代,直到簇心的移动距离小于某个给定的值。
K-Means聚类算法主要分为三个步骤:
(1)第一步是为待聚类的点寻找聚类中心
(2)第二步是计算每个点到聚类中心的距离,将每个点聚类到离该点最近的聚类中去
(3)第三步是计算每个聚类中所有点的坐标平均值,并将这个平均值作为新的聚类中心
反复执行(2)、(3),直到聚类中心不再进行大范围移动或者聚类次数达到要求为止
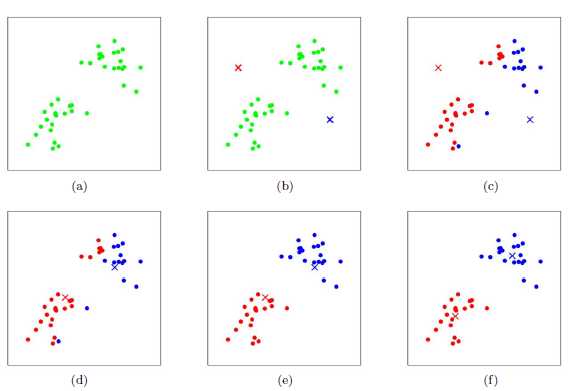
下图展示了对n个样本点进行K-means聚类的效果,这里k取2:
(a)未聚类的初始点集
(b)随机选取两个点作为聚类中心
(c)计算每个点到聚类中心的距离,并聚类到离该点最近的聚类中去
(d)计算每个聚类中所有点的坐标平均值,并将这个平均值作为新的聚类中心
(e)重复(c),计算每个点到聚类中心的距离,并聚类到离该点最近的聚类中去
(f)重复(d),计算每个聚类中所有点的坐标平均值,并将这个平均值作为新的聚类中心
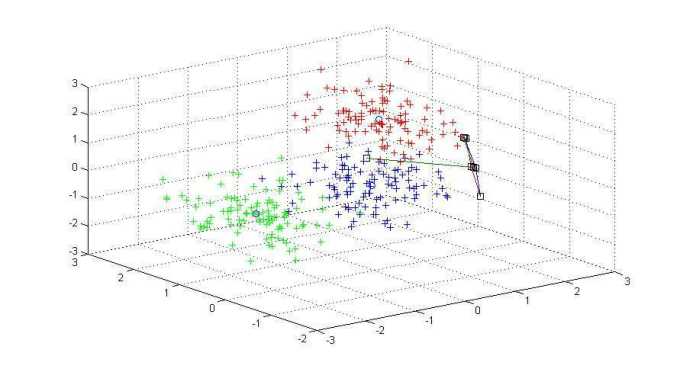
1 mu1=[0 0 0]; %均值 2 S1=[0.3 0 0;0 0.35 0;0 0 0.3]; %协方差 3 data1=mvnrnd(mu1,S1,100); %产生高斯分布数据 4 5 %%第二类数据 6 mu2=[1.25 1.25 1.25]; 7 S2=[0.3 0 0;0 0.35 0;0 0 0.3]; 8 data2=mvnrnd(mu2,S2,100); 9 10 %第三个类数据 11 mu3=[-1.25 1.25 -1.25]; 12 S3=[0.3 0 0;0 0.35 0;0 0 0.3]; 13 data3=mvnrnd(mu3,S3,100); 14 15 %显示数据 16 plot3(data1(:,1),data1(:,2),data1(:,3),‘+‘); 17 hold on; 18 plot3(data2(:,1),data2(:,2),data2(:,3),‘r+‘); 19 plot3(data3(:,1),data3(:,2),data3(:,3),‘g+‘); 20 grid on; 21 22 23 data=[data1;data2;data3]; 24 >> [u re]=kmeans(data,3); 25 [m n]=size(re); 26 >> for i=1:m 27 28 plot3(re(i,1),re(i,2),re(i,3),‘bo‘); 29 end
标签:
原文地址:http://www.cnblogs.com/cyp520918/p/4302253.html