平面上欧拉定理：poj 2284( LA 3263 ) That Nice Euler Circuit

标签：欧拉定理   计算几何   

Description

Input

Output

For each test case there will be one output line in the format 

Case x: There are w pieces., 

where x is the serial number starting from 1. 

Note: The figures below illustrate the two sample input cases. 

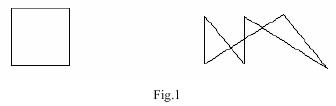
Sample Input

5
0 0 0 1 1 1 1 0 0 0
7
1 1 1 5 2 1 2 5 5 1 3 5 1 1
0

Sample Output

Case 1: There are 2 pieces.
Case 2: There are 5 pieces.

Source

题目大意

平面上给出n个点，求划分出的平面区域个数

解题思路

欧拉定理：设平面图的顶点数、边数和面数分别是V,E,F，则有V+F-E=2

●顶点个数v:n个顶点+交点，注意存在三线共点的情况，找到所有交点后要去重，利用去重函数unique去重函数unique

●棱数e：n条棱，若有交点棱数要多，注意存在三线共点的情况，并不是简单地一个交点就多以条棱，而是凡是穿过交点的边棱数都加+，所有要遍历边判断交点是否在边上，满足就e++

参考《算法竞赛入门经典——训练指南》第四章 计算几何

参考代码+部分注释

#include <iostream>
#include <cstdio>
#include <algorithm>
#include <map>
#include <vector>
#include <queue>
#include <cstring>
#include <cmath>
#include <climits>
#define eps 1e-10
using namespace std;
typedef long long ll;
const int INF=INT_MAX;
const int maxn = 300+10;
int dcmp(double x){//三态函数，克服浮点数精度陷阱，判断x==0?x<0?x>0?
  if(fabs(x)<eps) return 0;else return x<0?-1:1;
}
struct Point{
    double x,y;
    Point(double x=0,double y=0):x(x),y(y){}//构造函数，方便代码编写
};
typedef Point Vector;//Vector是 Point的别名

Vector operator + (Vector A,Vector B){return Vector(A.x+B.x,A.y+B.y);}
Vector operator - (Vector A,Vector B){return Vector(A.x-B.x,A.y-B.y);}
Vector operator * (Vector A,double p){return Vector(A.x*p,A.y*p);}
Vector operator / (Vector A,double p){return Vector(A.x/p,A.y/p);}
bool operator <(const Point& a,const Point& b){return a.x<b.x||(a.x==b.x&&a.y<b.y);}
bool operator ==(const Point& a,const Point& b){return dcmp(a.x-b.x)==0&&dcmp(a.y-b.y)==0;}

double Dot(Vector A,Vector B){return A.x*B.x+A.y*B.y;}
double Length(Vector A){return sqrt(Dot(A,A));}
double Angle(Vector A,Vector B){return acos(Dot(A,B)/Length(A)/Length(B));}
double Cross(Vector A,Vector B){return A.x*B.y-A.y*B.x;}
//向量旋转，rad是弧度不是角度
Vector Rotate(Vector A,double rad){return Vector(A.x*cos(rad)-A.y*sin(rad),A.x*sin(rad)+A.y*cos(rad));}
//直线交点，调用前请确保两条直线P+tv,Q+tw有唯一交点。当且仅当Cross（v,w）非0
Point GetLineIntersection(Point P,Vector v,Point Q,Vector w){
  Vector u=P-Q;
  double t=Cross(w,u)/Cross(v,w);
  return P+v*t;
}
//线段规范相交判定
bool SegmentProperIntersection(Point a1,Point a2,Point b1,Point b2){
  double c1=Cross(a2-a1,b1-a1),c2=Cross(a2-a1,b2-a1),
         c3=Cross(b2-b1,a1-b1),c4=Cross(b2-b1,a2-b1);
  return dcmp(c1)*dcmp(c2)<0 && dcmp(c3)*dcmp(c4)<0;
}
//点在线上（三点共线）判定
bool OnSegment(Point p,Point a1,Point a2){
 return dcmp(Cross(a1-p,a2-p))==0&&dcmp(Dot(a1-p,a2-p))<0;
}

Point P[maxn],V[maxn*maxn];//P[]存储n个点,v[]存储可能的顶点
int main()
{
 //  freopen("input.txt","r",stdin);
   int n,kase=0;
   while(scanf("%d",&n)==1&&n){
    for(int i=0;i<n;i++) {scanf("%lf%lf",&P[i].x,&P[i].y);V[i]=P[i];}
    n--;                                     //n个顶点，其中有一个重复，要减掉
    //求顶点个数v,初始为n,考虑到可能有三线共点的情况，求出所有交点再去重
    int v=n;
    for(int i=0;i<n;i++)
        for(int j=i+1;j<n;j++)
        if(SegmentProperIntersection(P[i],P[i+1],P[j],P[j+1]))
            V[v++]=GetLineIntersection(P[i],P[i+1]-P[i],P[j],P[j+1]-P[j]);
    sort(V,V+v);
    v=unique(V,V+v)-V;//去重过程，先排序；最终得到顶点数v
    //再求棱e,初始化e=n，注意三线共点的情况，并不是有几个交点棱就+几
    int e=n;
    for(int i=0;i<v;i++)
        for(int j=0;j<n;j++)
        if(OnSegment(V[i],P[j],P[j+1])) e++;//遍历边，点再线上说明出现交点，e++
    printf("Case %d: There are %d pieces.\n",++kase,e+2-v);
   }
   return 0;
}

平面上欧拉定理：poj 2284( LA 3263 ) That Nice Euler Circuit

标签：欧拉定理   计算几何   

原文地址：http://blog.csdn.net/u012717411/article/details/43985743