标签:
转自http://www.cnblogs.com/whatbeg/p/3765624.html
首先将原图中的连通分量缩点,一定可以将原图缩成一棵树的形式,然后统计这棵树的叶子节点个数,答案就是(leaf+1)/2。这里不再证明,可以画个图看一下。
(简单说明一下,首先把两个最近公共祖先最远的两个叶节点之间连接一条边,这样可以把这两个点到祖先的路径上所有点收缩到一起,因为一个形成的环一定是双连通的。然后再找两个最近公共祖先最远的两个叶节点,这样一对一对找完,恰好是(leaf+1)/2次,把所有点收缩到了一起。 --Byvoid)
怎么统计呢?用并查集缩点,可以知道,缩点后留下的边全部是原图的桥,这是我们可以用Tarjan求出原图的所有桥,然后枚举每条桥,桥两端的点度数分别+1,就可以求出每个点(缩点后的点)的度数了,找出度数为1的即为叶子节点。
怎么用Tarjan求桥呢?根据Tarjan算法性质可知,若low[v]>dfn[u],则边(u,v)为桥(v被封死在子树内)
如图,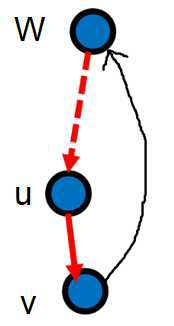 若low[v]>dfn[u],则v被封死在u的子树内,删除点u,或者删除边(u,v),都将使v与u的祖先w不连通。
若low[v]>dfn[u],则v被封死在u的子树内,删除点u,或者删除边(u,v),都将使v与u的祖先w不连通。
关于Tarjan求桥可见:http://hi.baidu.com/lydrainbowcat/item/f8a5ac223e092b52c28d591c
1 #include<iostream> 2 #include<cstdio> 3 #include<cstdlib> 4 #include<cstring> 5 #include<string> 6 #include<queue> 7 #include<algorithm> 8 #include<map> 9 #include<iomanip> 10 #include<climits> 11 #include<string.h> 12 #include<cmath> 13 #include<stdlib.h> 14 #include<vector> 15 #include<stack> 16 #define INF 1000000007 17 #define MAXN 40010 18 #define Mod 1000007 19 #define N 10010 20 #define NN 30 21 #define sigma_size 3 22 const int maxn = 6e5 + 10; 23 using namespace std; 24 typedef long long LL; 25 26 struct Bridge { 27 int u, v; 28 }bg[2*N]; 29 30 vector<int> G[N]; 31 int vis[N], low[N], dfn[N], Time; 32 int fa[N], deg[N]; 33 int n, m, cnt; 34 int u, v; 35 36 int findset(int x) 37 { 38 return fa[x] = fa[x] == x ? x : findset(fa[x]); 39 } 40 41 void init() 42 { 43 for (int i = 0; i <= n; ++i) { 44 G[i].clear(); 45 fa[i] = i; 46 } 47 memset(dfn,0,sizeof(dfn)); 48 memset(low,0,sizeof(low)); 49 memset(vis,0,sizeof(vis)); 50 memset(deg, 0, sizeof(deg)); 51 cnt = Time = 0; 52 for (int i = 0; i < m;++ i) { 53 cin >> u >> v; 54 G[u].push_back(v); 55 G[v].push_back(u); 56 } 57 } 58 59 void Tarjan(int u, int father) 60 { 61 low[u] = dfn[u] = ++Time; 62 vis[u] = 1; 63 for (int i = 0; i < G[u].size(); ++i) { 64 int v = G[u][i]; 65 if (v == father) continue; 66 if (!vis[v]){ 67 Tarjan(v, u); 68 low[u] = min(low[u], low[v]); 69 if (low[v] > dfn[u]){ //u->v为桥 70 bg[cnt].u = u; 71 bg[cnt].v = v; 72 cnt++; 73 } 74 else { //否则u,v同属一个连通分量,合并 75 int fx = findset(u); 76 int fy = findset(v); 77 if (fx != fy) 78 fa[fx] = fy; 79 } 80 } 81 else { 82 low[u] = min(low[u],dfn[v]); 83 } 84 } 85 } 86 87 int main() 88 { 89 while (cin >> n >> m) { 90 init(); 91 Tarjan(1,-1); 92 for (int i = 0; i < cnt; ++i) { 93 int fx = findset(bg[i].u); 94 int fy = findset(bg[i].v); 95 deg[fx]++; 96 deg[fy]++; 97 } 98 int leaf = 0; 99 for (int i = 1; i <= n; ++i) 100 if(deg[i] == 1) leaf++; 101 cout << (leaf + 1) / 2 << endl; 102 } 103 //system("pause"); 104 return 0; 105 }
标签:
原文地址:http://www.cnblogs.com/usedrosee/p/4305974.html