Hihocoder #1121 二分图一?二分图判定( bfs或者dfs搜索实现 搜索的过程中进行 节点标记 *【模板】)

标签：

对于拿到的相亲情况表，我们不妨将其转化成一个图。将每一个人作为一个点(编号1..N)，若两个人之间有一场相亲，则在对应的点之间连接一条无向边。(如下图)

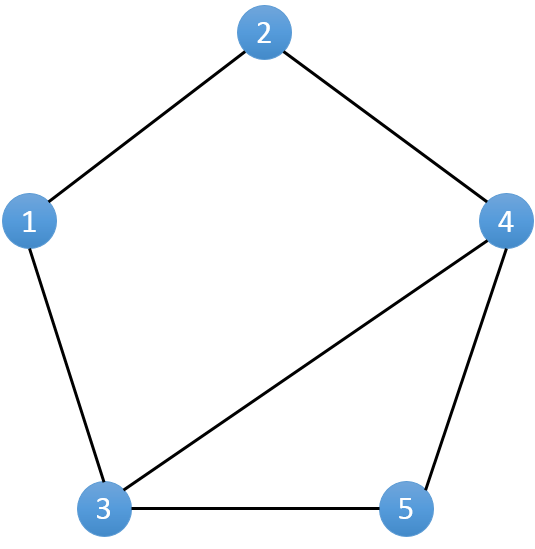
因为相亲总是在男女之间进行的，所以每一条边的两边对应的人总是不同性别。假设表示男性的节点染成白色，女性的节点染色黑色。对于得到的无向图来说，即每一条边的两端一定是一白一黑。如果存在一条边两端同为白色或者黑色，则表示这一条边所表示的记录有误。

由于我们并不知道每个人的性别，我们的问题就转化为判定是否存在一个合理的染色方案，使得我们所建立的无向图满足每一条边两端的顶点颜色都不相同。

那么，我们不妨将所有的点初始为未染色的状态。随机选择一个点，将其染成白色。再以它为起点，将所有相邻的点染成黑色。再以这些黑色的点为起点，将所有与其相邻未染色的点染成白色。不断重复直到整个图都染色完成。(如下图)

在染色的过程中，我们应该怎样发现错误的记录呢？相信你一定发现了吧。对于一个已经染色的点，如果存在一个与它相邻的已染色点和它的颜色相同，那么就一定存在一条错误的记录。(如上图的4，5节点)

整个图的算法：

1. 选取一个未染色的点u进行染色。

2. 遍历u的相邻节点v：若v未染色，则染色成与u不同的颜色，并对v重复第2步；若v已经染色，如果 u和v颜色相同，判定不可行退出遍历。

3. 若所有节点均已染色，则判定可行。

样例输入

2
5 5
1 2
1 3
3 4
5 2
1 5
5 5
1 2
1 3
3 4
5 2
3 5

样例输出

Wrong
Correct

#include <stdio.h>
#include <string.h>
#include <stdlib.h>
#include <vector>
#include <queue>

#define N 10001

using namespace std;
int n, m;
vector<int>q[N];
int flag[N];
bool vis[N];
bool bfs(int dd)
{
    //0代表未着色，1代表白色，2代表黑色

    queue<int>p;
    while(!p.empty()) p.pop();
    p.push(dd);
    flag[dd]=1;
    vis[dd]=true;
    while(!p.empty())
    {
        int dd=p.front(); p.pop();
        //printf("%d***", dd);

        for(int i=0; i<q[dd].size(); i++)
        {
            if(flag[q[dd][i]]==0 )
            {
                flag[q[dd][i]] = flag[dd]==1?2:1;
                p.push(q[dd][i]);
            }
            else if(flag[q[dd][i]] == flag[dd] )
            {
                return false;
            }
        }
    }
    return true;
}
bool is_bi()
{
    for(int i=1;i<=n;i++){
        if(!flag[i])
        {
            flag[i] = 1;
            if(!bfs(i))
                return false;
        }
    }
    return true;
}


int main()
{
    int i, j, u, v;
    int t;
    scanf("%d", &t);
    while(t--)
    {
        scanf("%d %d", &n, &m);
        for(i=1; i<=n; i++)
            q[i].clear();
        for(i=0; i<m; i++)
        {
            scanf("%d %d", &u, &v);
            q[u].push_back(v);
            q[v].push_back(u); //建立无向图
        }
        memset(flag, 0, sizeof(flag));
        if(is_bi())
            printf("Correct\n");
        else
            printf("Wrong\n");
    }
    return 0;
}

 

Hihocoder #1121 二分图一?二分图判定( bfs或者dfs搜索实现 搜索的过程中进行 节点标记 *【模板】)

标签：

原文地址：http://www.cnblogs.com/yspworld/p/4306593.html