标签:
题目:
Farm Irrigation |
| Time Limit: 2000/1000 MS (Java/Others) Memory Limit: 65536/32768 K (Java/Others) |
| Total Submission(s): 202 Accepted Submission(s): 104 |
Problem Description Benny has a spacious farm land to irrigate. The farm land is a rectangle, and is divided into a lot of samll squares. Water pipes are placed in these squares. Different square has a different type of pipe. There are 11 types of pipes, which is marked from A to K, as Figure 1 shows. 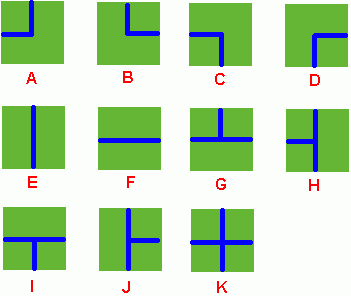 Benny has a map of his farm, which is an array of marks denoting the distribution of water pipes over the whole farm. For example, if he has a map ADC FJK IHE then the water pipes are distributed like 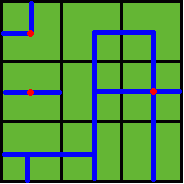 Several wellsprings are found in the center of some squares, so water can flow along the pipes from one square to another. If water flow crosses one square, the whole farm land in this square is irrigated and will have a good harvest in autumn. Now Benny wants to know at least how many wellsprings should be found to have the whole farm land irrigated. Can you help him? Note: In the above example, at least 3 wellsprings are needed, as those red points in Figure 2 show. |
Input There are several test cases! In each test case, the first line contains 2 integers M and N, then M lines follow. In each of these lines, there are N characters, in the range of ‘A‘ to ‘K‘, denoting the type of water pipe over the corresponding square. A negative M or N denotes the end of input, else you can assume 1 <= M, N <= 50. |
Output For each test case, output in one line the least number of wellsprings needed. |
Sample Input 2 2 DK HF 3 3 ADC FJK IHE -1 -1 |
Sample Output 2 3 |
Author ZHENG, Lu |
Source Zhejiang University Local Contest 2005 |
Recommend Ignatius.L |
题目大意:
有一个矩阵,这个剧震里面有n*m个小方块。每个方块都可以铺一种水管。为了让所有小方块都有谁能够灌溉得到,求至少需要打多少口井。
题目分析:
并查集,简单题。在之前我们做过的题中,如果出现"a b"这样的数据,就代表这两个节点连通。但是在
这道题中map[][]中相邻的两个节点不一定连通,需要满足一定条件的情况下才连通。对于这个n*m的矩阵,每个节点
只需要两个方向上是否能够合并即可(右边和下边)。
代码如下:
/*
* d.cpp
*
* Created on: 2015年3月2日
* Author: Administrator
*/
#include <iostream>
#include <cstdio>
using namespace std;
const int maxn = 51;
int father[maxn*maxn];//用于保存父子关系
char map[maxn][maxn];//地图信息.如map[0][0]=‘B‘表示的是第0行第0列这个小方块用的是B这种类型的水管
//用于标叔各种类型的水管的特点.1表示有水管铺到
int type[11][4] = { { 1, 1, 0, 0 }, { 0, 1, 1, 0 }, { 1, 0, 0, 1 },
{ 0, 0, 1, 1 }, { 0, 1, 0, 1 }, { 1, 0, 1, 0 }, { 1, 1, 1, 0 }, { 1, 1,
0, 1 }, { 1, 0, 1, 1 }, { 0, 1, 1, 1 }, { 1, 1, 1, 1 } };
bool VERTICAL = true;//判断是否在垂直方向
int n,m;//n:行数.m:列数
int cnt;//集合的个数
/**
* 判断坐标是否合法
*/
bool check(int x,int y){
if(x < 0 || x >= n || y < 0 || y >= m){//如果坐标已经越界
return false;//返回false
}
return true;//返回true
}
/**
* 初始化父子关系
*/
void init(){
int i;
for(i = 0 ; i < maxn*maxn ; ++i){//遍历所有的结点.(需要注意的是,如果有问题,i尽量不要从0开始)
father[i] = i;//所有节点的父亲默认都是他自己
}
}
/**
* 查找一个节点所在集合的根节点
*/
int find(int a){
if(a == father[a]){//如果一个节点的父亲是它自己
return a;//则这个节点就是所要找的根节点
}
return father[a] = find(father[a]);//否则继续寻找根节点
}
/**
* 合并两个节点
* x1,y1:一个节点的横纵坐标
* x2,y2:另一个节点的横纵坐标
* dir:用于标记是否是垂直方向
*/
void join(int x1,int y1,int x2,int y2,bool dir){
if(check(x2,y2) == false){//如果第二个节点的坐标不合法
return ;//则直接返回
}
int t1 = map[x1][y1] - ‘A‘;//计算第一个节点的水管类型
int t2 = map[x2][y2] - ‘A‘;//计算第二个节点的水管类型
bool flag = false;//用于标记两个节点是否连通,默认为false
if(dir == true){//如果是垂直方向
//则判断第一个节点的下方和第二个节点的上方是否同时有水管
if(type[t1][3] == 1 && type[t2][1] == 1){
flag = true;//如果都有的话,则将flag标记为true,表示这两个节点连通
}
}else{//如果不是垂直方向
//则判断第一个节点的右方和第二个节点的结点的左方是否同事有水管
if(type[t1][2] == 1 && type[t2][0] == 1){
flag = true;//如果都有的话,则将flag标记为true,表示这两个节点连通
}
}
if(flag == true){//如果两个节点连通,则将他们合并
int a = x1*m + y1;//将二维坐标转换成一维坐标
int b = x2*m + y2;
int fa = find(a);
int fb = find(b);
if(fa != fb){
father[fa] = fb;//合并两个结合
cnt--;//将集合总数减一
}
}
}
int main() {
while(scanf("%d%d",&n,&m)!=EOF,n >= 0){
init();//初始化父子关系
cnt = n*m;//初始化集合数。默认是n*m
int i;
for(i = 0 ; i < n ; ++i){
cin >> map[i];
}
int j;
for(i = 0 ; i < n ; ++i){
for(j = 0 ; j < m ; ++j){
join(i,j,i+1,j,VERTICAL);//合并一个节点和它下方的节点
join(i,j,i,j+1,!VERTICAL);//合并一个节点和它右边的节点
}
}
printf("%d\n",cnt);
}
return 0;
}
(hdu step 5.1.4)Farm Irrigation(在两个节点合并有限制条件的情况下,求集合的个数)
标签:
原文地址:http://blog.csdn.net/hjd_love_zzt/article/details/44022153