标签:c style class blog code java
算法简介
前面介绍过图的单源最短路径算法Dijkstra算法,然而Dijkstra算法无法判断含负权边的图的最短路。如果遇到负权,在没有负权回路存在时(负权回路的含义是,回路的权值和为负。)即便有负权的边,也可以采用Bellman-Ford算法正确求出最短路径。
Bellman-Ford算法能在更普遍的情况下(存在负权边)解决单源点最短路径问题。对于给定的带权(有向或无向)图G=(V,E),其源点为s,加权函数
w是 边集 E
的映射。对图G运行Bellman-Ford算法的结果是一个布尔值,表明图中是否存在着一个从源点s可达的负权回路。若不存在这样的回路,算法将给出从源点s到
图G的任意顶点v的最短路径d[v]。
Bellman-Ford算法能在更普遍的情况下(存在负权边)解决单源点最短路径问题。对于给定的带权(有向或无向)图G=(V,E),其源点为s,加权函数 w是 边集 E 的映射。对图G运行Bellman-Ford算法的结果是一个布尔值,表明图中是否存在着一个从源点s可达的负权回路。若不存在这样的回路,算法将给出从源点s到 图G的任意顶点v的最短路径d[v]。
适用条件&范围
算法流程
参考代码实现:
此处为有向图的实现,要验证,只需在main()函数下运行test_BellmanFord()函数即可。
#include<iostream> using namespace std; const int MaxEdges= 100; const int MaxVertex= 20; const int MaxWeight= 10000; struct MyEdge { int v1,v2; int weight; MyEdge() { v1 = -1; v2 = -1; weight = MaxWeight; } }; struct MyGraph { MyEdge edges[MaxEdges]; int NumVertex; int NumEdges; }; void createGraph(MyGraph *mg) { cout<<"请输入顶点数和边数:"<<endl; cin>>mg->NumVertex >>mg->NumEdges; cout<<"请依次输入各边权重(v1,v2,weight):"<<endl; int v1,v2 ,weight; for (int j=0;j<mg->NumEdges;j++) { cin>>v1>>v2>>weight; mg->edges[j].v1=v1; mg->edges[j].v2=v2; mg->edges[j].weight = weight; } } bool Bellman_ford(MyGraph *mg,int s,int *dis,int *pre) { int numV = mg->NumVertex; for(int i = 0;i<numV;i++) //初始化距离 { dis[i] = (i==s)? 0:MaxWeight; pre[i] = -1; //前一个点初始为-1 } pre[s]=s; for(int i=1;i<numV;i++)//松弛操作 { for(int j=0;j<mg->NumEdges;j++) { if(dis[mg->edges[j].v2] > dis[mg->edges[j].v1] + mg->edges[j].weight) { dis[mg->edges[j].v2] = dis[mg->edges[j].v1] + mg->edges[j].weight; pre[mg->edges[j].v2] = mg->edges[j].v1; } } } for(int j=0;j<mg->NumEdges;j++)//判断是否含有负权回路 { if(dis[mg->edges[j].v2] > dis[mg->edges[j].v1] + mg->edges[j].weight) return false; } return true; } void print_path( int j,int *pre) { while(pre[j]!=-1 && pre[j]!= j) { cout<<j<<"-->"; j=pre[j]; } if(j ==pre[j]) cout<<j; } void test_BellmanFord() { int dis[MaxVertex];// int pre[MaxVertex]; MyGraph MG; createGraph(&MG); cout<<"输入Bellman_ford算法的起点:"; int start; cin>>start; if(Bellman_ford(&MG,start,dis,pre)) { for(int j=0;j<MG.NumVertex;j++) { cout<<"到点"<<j <<"的最短路径:"<<dis[j]<<endl; cout<<"路径:"; print_path(j,pre); cout<<endl; } } else cout<<"存在负权环,算法无法实行!"<<endl; }
运行结果样例:
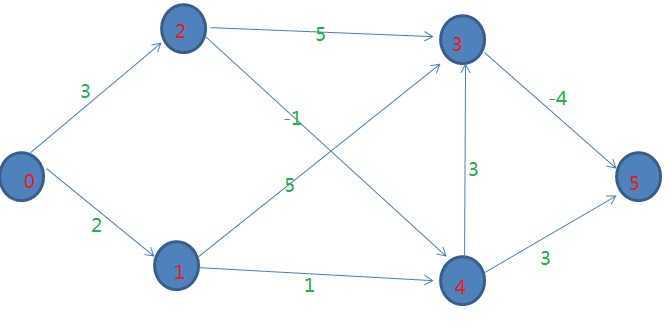
带负权图的单源最短路径算法:Bellman-Ford算法,布布扣,bubuko.com
标签:c style class blog code java
原文地址:http://www.cnblogs.com/f8master/p/3762529.html