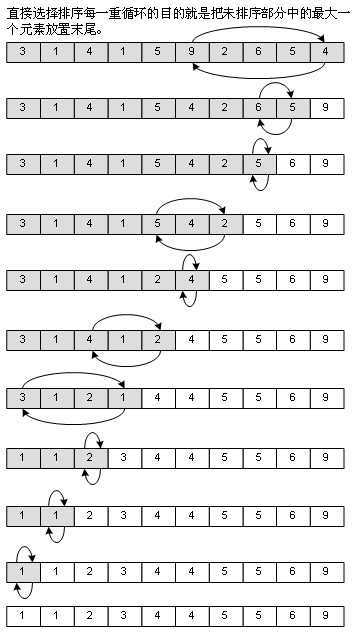
i从0开始,默认本趟最小的位置min_index为i,若第min_index大于第i+1、i+2直到n-1,则修改min_index为i+1、i+2...n-1,若min_index不等于i,则交换位置。重复n-1次,完成排序。
比较操作为n(n-1)/2次,即O(n^2);交换操作介于0和(n-1)次,即O(n);赋值操作介于0和3(n-1)次,即O(n)。主要优点在于数据的移动,如果某个元素位于正确的最终位置上,则它不会被移动。选择排序每次交换一对元素,它们当中至少有一个将被移到其最终位置上,因此对n个元素的表进行排序总共进行至多n-1次交换。在所有的完全依靠交换去移动元素的排序方法中,选择排序属于非常好的一种。

1 def selection_sort(data): 2 for i in range(len(data)): 3 min_index = i 4 for j in range(i+1,len(data)): 5 if data[min_index] > data[j]: 6 min_index = j 7 if min_index <> i: 8 data[i],data[min_index] = data[min_index],data[i]
将序列调整成堆,交换堆顶元素与最后一个节点元素,将最后一个节点剔除出堆,再将剩下序列调整成堆,然后再交换堆顶元素与最后一个节点元素...

1 def heap_adjust(data,s,m): 2 if 2*s > m: 3 return 4 temp = s-1 5 if data[2*s-1] > data[temp]: 6 temp = 2*s-1 7 if 2*s <= m-1 and data[2*s] > data[temp]: 8 temp = 2*s 9 if temp <> s-1: 10 data[s-1],data[temp] = data[temp],data[s-1] 11 heap_adjust(data,temp+1,m) 12 13 def heap_sort(data): 14 for i in range(len(data)/2,0,-1): 15 heap_adjust(data,i,len(data)) 16 data[0],data[-1] = data[-1],data[0] 17 for n in range(len(data)-1,1,-1): 18 heap_adjust(data,1,n) 19 data[0],data[n-1] = data[n-1],data[0]
i从1开始,待插入tmp为第i,若tmp小于第i-1、i-2...0,则第i-1、i-2...0移动到第i,i-1...1,tmp插入第i-1、i-2...0。此时,第0...第i有序,第i+1...n-1无序。重复n-1次,完成排序。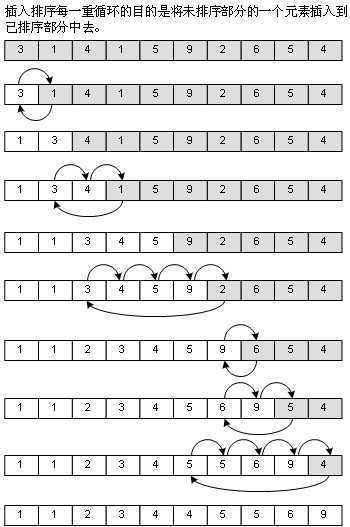

1 def insertion_sort(data): 2 for i in range(1,len(data)): 3 tmp = data[i] 4 j = i-1 5 while data[j] > tmp and j >= 0: 6 data[j+1] = data[j] 7 j = j-1 8 if j <> i-1: 9 data[j+1] = tmp
将序列分割为若干相隔increament的子序列,对各个子序列进行插入排序;再选择一个更小的increment,再将序列分割为多个子序列进行排序...直到increment为1,最终序列有序。
O(n的1.5次方),不稳定排序。把待排序序列分成若干较小的子序列,然后逐个使用直接插入排序法排序,最后再对一个较为有序的序列进行一次排序,比直接从无序到有序移动的次数少,提高效率。

1 def shell_sort(data,step=None): 2 if step == None: 3 step = len(data)//2 4 for i in range(0,step): 5 subdata = data[i:len(data):step] 6 insertion_sort(subdata) 7 data[i:len(data):step] = subdata 8 if step <> 1: 9 step = step//2 10 shell_sort(data,step)
i从0开始,若第i大于第i+1,则交换位置,直到第n-i-2和第n-i-1。此时,第n-i-1为本趟最大。重复n-1次,即n-i-1为0时,完成排序。
o(n^2),稳定排序,适合规模比较小数据。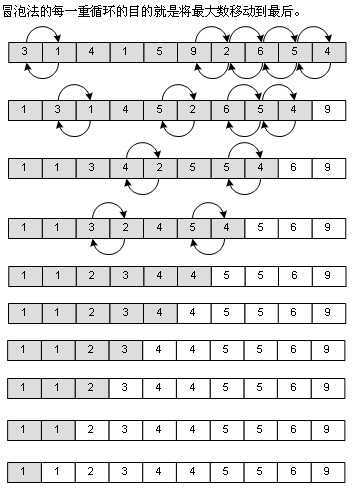

1 def bubble_sort(data): 2 for i in range(len(data)): 3 for j in range(len(data)-i-1): 4 if data[j] > data[j+1]: 5 data[j],data[j+1] = data[j+1],data[j]
1.
选择序列的第1个元素作为基准standard,比standard大的放在基准右边,比standard小的放在基准左边,最终移动standard,形成standard前和standard后的两个子序列;
2
递归地选择子序列的第一个元素作为子序列的子基准standard,划分子子序列。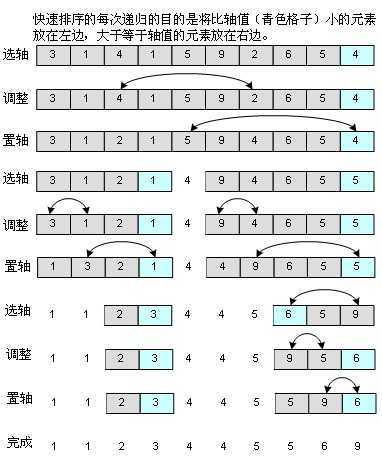

1 def quick_sort(data,low=0,high=None): 2 if high==None: 3 high = len(data)-1 4 if low < high: 5 standard,left,right = data[low],low,high 6 while left < right: 7 while data[right] > standard and left < right: 8 right = right-1 9 if left < right: 10 data[left] = data[right] 11 left = left+1 12 while data[left] <= standard and left < right: 13 left = left+1 14 if left < right: 15 data[right] = data[left] 16 data[left] = standard 17 quick_sort(data,low,left-1) 18 quick_sort(data,left+1,high)

1 import random,datetime,copy 2 3 def sort_perform(sort,data): 4 sort_data = copy.deepcopy(data) 5 t1 = datetime.datetime.now() 6 sort(sort_data) 7 t2 = datetime.datetime.now() 8 print sort.__name__, ‘\t‘, t2-t1 9 10 if __name__ == ‘__main__‘: 11 data = [random.randint(0,65535) for i in range(3000)] 12 sort_perform(selection_sort,data) 13 sort_perform(heap_sort,data) 14 sort_perform(insertion_sort,data) 15 sort_perform(shell_sort,data) 16 sort_perform(bubble_sort,data) 17 sort_perform(quick_sort,data)
从[0,65535)中随机抽取3000个数(有重复),测试结果为:
selection_sort 0:00:00.629048
heap_sort 0:00:00.055195
insertion_sort 0:00:00.730729
shell_sort 0:00:00.035422
bubble_sort 0:00:01.510431
quick_sort 0:00:00.017847
原文地址:http://www.cnblogs.com/huangavoid/p/3762722.html