标签:
当我看到蔡氏电路所生成的混沌图像时,有了这样的感受:写程序会有一种如在坑中的感觉,好不容易从一个坑里爬了出来,又落入另一个坑中。始终处于不停地纠结中,不知道什么时候可以结束。
蔡氏电路(英语:Chua‘s circuit),一种简单的非线性电子电路设计,它可以表现出标准的混沌理论行为。在1983年,由蔡少棠教授发表。这个电路的制作容易程度使它成为了一个无处不在的现实世界的混沌系统的例子,一些人声明它是一个“混沌系统的典范”。它在(x,y,z)空间的形状, 被首次观察到在电子线路中包含一个非线性元件。通过电磁学定律的应用,蔡氏电路可以被准确的建立数学模型:这是变量x(t), y(t),和z(t)的一个三个非线性常微分方程的系统,分别是在电容C1和C2上的电压,和在电感L1上的电流强度。蔡氏方程有:
dx = a*[y-x-f(x)]
dy = x-y+z
dz = -b*y
函数 f(x) 描述了非线性电阻的电子响应,并且它的形状是依赖于它的元件的特定配置。
如:f(x)=cx(t)+0.5(d-c)(|x(t)+1|-|x(t)-1|)
参数 α 和 β 是由电路元件的特定值来决定的。
蔡氏电路采用非线性,是直观地演示混沌现象一个非常好的选择。
能产生混沌现象的自治电路至少要满足三个条件:
(1)有一个非线性元件
(2)有一个用于耗散能量的电阻
(3)有三个存储能量的元件。
蔡氏电路即满足上述条件。因为其结构简单、现象清晰,所以经常用于观察混沌现象。
作为一个最简单的实验实现的电路,并且存在一种简单而准确的理论模型相结合,使蔡氏电路成为一个研究混沌理论的许多基础研究和应用的问题的实用系统。正因为如此,它一直是许多研究的对象,并广泛被人们在文献中引用。
这里使用自己定义语法的脚本代码生成混沌图像.相关软件参见:YChaos生成混沌图像.如果你对数学生成图形图像感兴趣,欢迎加入QQ交流群: 367752815
脚本代码:
[ScriptLines] l=sqrt(x^2+y^2) x=if(l<0.01, x/l, x) y=if(l<0.01, y/l, y) f=c*x + 0.5*(d-c)*(abs(x+1)-abs(x-1)) u=a*(y - x - f) v=x - y + z w=-b*y x=x+u*t y=y+v*t z=z+w*t [Variables] a=3.000000 b=1.000000 c=2.000000 d=0.500000 t=0.001000 x=0.100000 y=0.300000 z=-0.600000


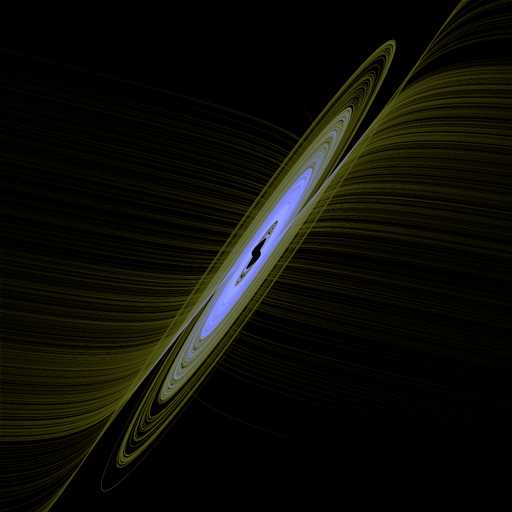
另一种写法
[ScriptLines] p=[static]sin(w) q=[static]cos(w) h=e*i + d*i*abs(i) + c*i*i*i u=a*(k - h) v=i - k + j w=-b*k i=i+u*t j=j+w*t k=k+v*t x=i*q - j*p y=i*p + j*q z=k [Variables] a=12.800000 b=19.100000 c=0.450000 d=-1.100000 e=0.600000 i=0.100000 j=0.300000 k=-0.600000 t=0.001000 w=0.861700
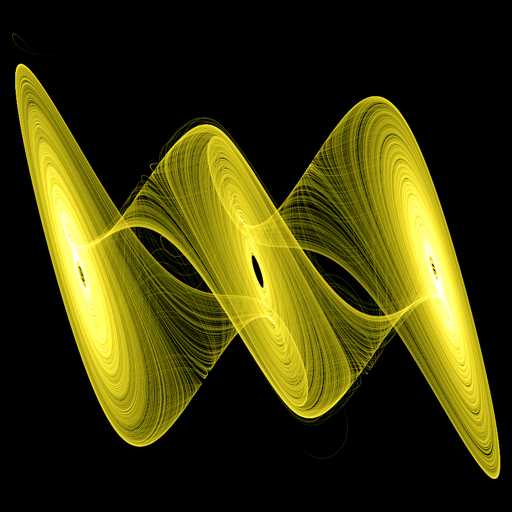
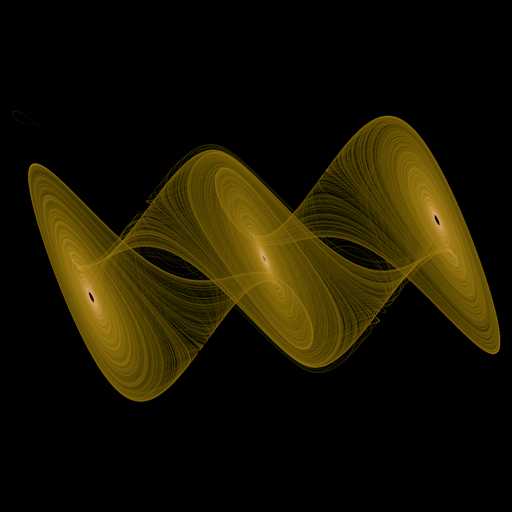
超混沌蔡氏吸引子
[ScriptLines] h=-b*sin(PI*x/2/a + d) u=m*(y - h) v=x - y + z w=-n*y x=x+u*t y=y+v*t z=z+w*t [Variables] a=1.300000 b=0.110000 d=0.000000 m=10.820000 n=14.286000 t=0.001000 x=1.000000 y=1.000000 z=0.000000
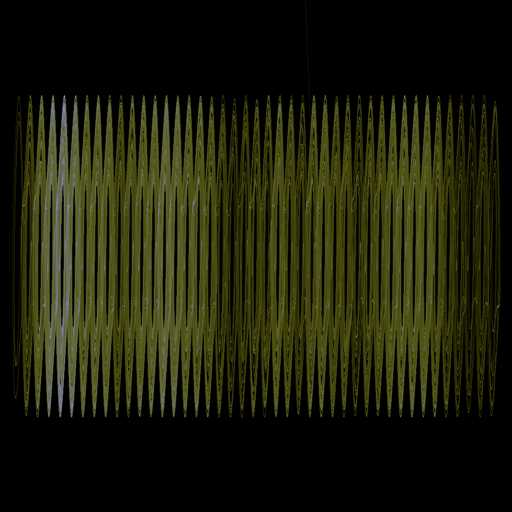

超混沌蔡氏吸引子看上去真是一个坑接着一个坑,永远没有结束的样子。
相关软件介绍:
相关文章:
标签:
原文地址:http://www.cnblogs.com/WhyEngine/p/4310746.html