标签:
文章参考:源码
这篇文章在一个偶然的机会看到,我原先也是知道sort函数效率高,但终究没有去了解原因,读了这篇文章更加钦佩C++大师积年累月智慧的结晶和对效率的极致追求,看到很多地方不禁暗暗称奇。也还是感慨原文作者对技术的追求和细致的讲解,下面的内容大多来自作者的文章,其中加入了自己的理解,也不枉费大半个下午的时间。
从事程序设计行业的朋友一定对排序不陌生,它从我们刚刚接触数据结构课程开始便伴随我们左右,是需要掌握的重要技能。任何一本数据结构的教科书一定会介绍各种各样的排序算法,比如最简单的冒泡排序、插入排序、希尔排序、堆排序等。在现已知的所有排序算法之中,快速排序名如其名,以快速著称,它的平均时间复杂度可以达到O(NlogN),是最快排序算法之一。
在校期间,为了掌握这些排序算法,我们不得不经常手动实现它们,以加深对其的理解。然而这些算法实在是太常用了,我们不太可能在每次需要时都手动来实现,不管是性能还是安全性都得不到保证。因此这些算法被包含进了很多语言的标准库里,在C语言的标准库中,stdlib.h头文件就有sort算法,它正是最快排序算法——快速排序的标准实现,这给我们提供了很大的方便。
然而,快速排序虽然平均复杂度为O(N logN),却可能由于不当的pivot选择,导致其在最坏情况下复杂度恶化为O(N2)。另外,由于快速排序一般是用递归实现,我们知道递归是一种函数调用,它会有一些额外的开销,比如返回指针、参数压栈、出栈等,在分段很小的情况下,过度的递归会带来过大的额外负荷,从而拉缓排序的速度。
为了解决快速排序在最坏情况下复杂度恶化的问题,人们进行了大量的研究,获得了众多研究成果。本文将要介绍的算法便是其中之一。在开始之前我们需要先简短介绍两个其它常用的算法,这对我们理解新算法为何如此设计非常重要,它们是堆排序和插入排序。
堆排序经常是作为快速排序最有力的竞争者出现,它们的复杂度都是O(N logN)。这里有一个维基百科上的动态图片,直观的反应出堆排序的过程:
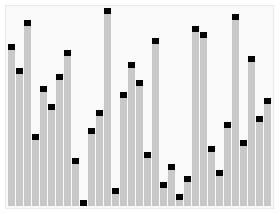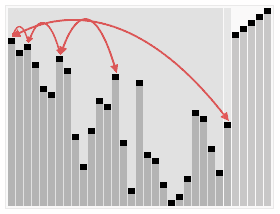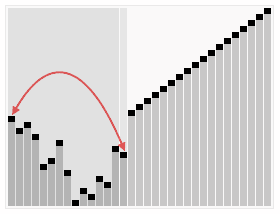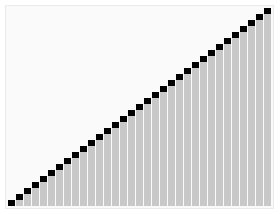
虽然两者拥有一样的复杂度,但就平均表现而言,它却比快速排序慢了2~5倍,知乎上有一个讨论:堆排序缺点何在?
但是,有一点它却比快速排序要好很多:最坏情况它的复杂度仍然会保持O(N logN)这一优点对本文介绍的新算法有着巨大的作用。
再来看看插入排序,同样有一张维基百科上的动态图片,可以唤起你对它的记忆:
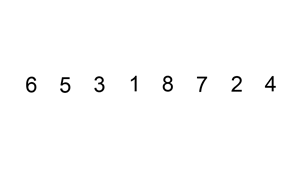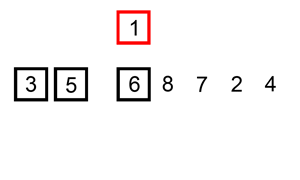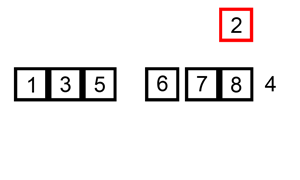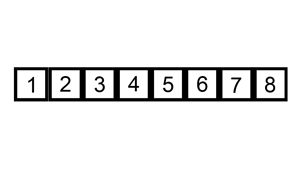
它在数据大致有序的情况表现非常好,可以达到O(N),可以参考这个讨论Which sort algorithm works best on mostly sorted data? 这一优点也被新算法所采用。
到了正式介绍新算法的时刻。由于快速排序有着前面所描述的问题,因此Musser在1996年发表了一遍论文,提出了Introspective Sorting(内省式排序),这里可以找到PDF版本。它是一种混合式的排序算法,集成了前面提到的三种算法各自的优点:
O(logN)。O(N)。O(N logN),但这又比一开始使用堆排序好。由此可知,它乃综合各家之长的算法。也正因为如此,C++的标准库就用其作为std::sort的标准实现。
SGI版本的STL一直是评价最高的一个STL实现,在技术层次、源代码组织、源代码可读性上,均有卓越表现。所以它被纳为GNU C++标准程序库。这里选择了侯捷的《STL源码剖析》一书中分析的GNU C++ 2.91版本来作分析,此版本稳定且可读性强。
std::sort的代码如下:
template <class RandomAccessIterator>
inline void sort(RandomAccessIterator first, RandomAccessIterator last) {
if (first != last) {
__introsort_loop(first, last, value_type(first), __lg(last - first) * 2);
__final_insertion_sort(first, last);
}
}它是一个模板函数,只接受随机访问迭代器。if语句先判断区间有效性,接着调用__introsort_loop,它就是STL的Introspective Sort实现。在该函数结束之后,最后调用插入排序。我们来揭开该算法的面纱:
template <class RandomAccessIterator, class T, class Size>
void __introsort_loop(RandomAccessIterator first,
RandomAccessIterator last, T*,
Size depth_limit) {
while (last - first > __stl_threshold) {
if (depth_limit == 0) {
partial_sort(first, last, last);
return;
}
--depth_limit;
RandomAccessIterator cut = __unguarded_partition
(first, last, T(__median(*first, *(first + (last - first)/2),
*(last - 1))));
__introsort_loop(cut, last, value_type(first), depth_limit);
last = cut;
}
}这是算法主体部分,代码虽然不长,但充满技巧,有很多细节需要注意,接下来我们将对其一一展开分析。
可以看出它是一个递归函数,因为我们说过,Introspective Sort在数据量很大的时候采用的是正常的快速排序,因此除了处理恶化情况以外,它的结构应该和快速排序一致。但仔细看以上代码,先不管循环条件和if语句(它们便是处理恶化情况所用),循环的后半部分是用来递归调用快速排序。但它与我们平常写的快速排序有一些不同,对比来看,以下是我们平常所写的快速排序的伪代码:
function quicksort(array, left, right)
// If the list has 2 or more items
if left < right
// See "#Choice of pivot" section below for possible choices
choose any pivotIndex such that left ≤ pivotIndex ≤ right
// Get lists of bigger and smaller items and final position of pivot
pivotNewIndex := partition(array, left, right, pivotIndex)
// Recursively sort elements smaller than the pivot (assume pivotNewIndex - 1 does not underflow)
quicksort(array, left, pivotNewIndex - 1)
// Recursively sort elements at least as big as the pivot (assume pivotNewIndex + 1 does not overflow)
quicksort(array, pivotNewIndex + 1, right)__introsort_loop中只有对右边子序列进行递归调用是不是?左边的递归不见了。的确,这里的写法可读性相对来说比较差,但是仔细一分析发现是有它的道理的,它并不是没有管左子序列。注意看,在分割原始区域之后,对右子序列进行了递归,接下来的last = cut将终点位置调整到了分割点,那么此时的[first, last)区间就是左子序列了。又因为这是一个循环结构,那么在下一次的循环中,左子序列便得到了处理。只是并未以递归来调用。
我们来比较一下两者的区别,试想,如果一个序列只需要递归两次便可结束,即它可以分成四个子序列。原始的方式需要两个递归函数调用,接着两者各自调用一次,也就是说进行了7次函数调用,如下图左边所示。但是STL这种写法每次划分子序列之后仅对右子序列进行函数调用,左边子序列进行正常的循环调用,如下图右边所示。
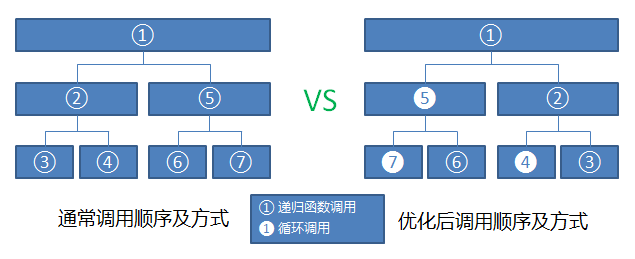
两者区别就在于STL节省了接近一半的函数调用,由于每次的函数调用有一定的开销,因此对于数据量非常庞大时,这一半的函数调用可能能够省下相当可观的时间。真是为了效率无所不用其极,令人惊叹!更关键是这并没有带来太多的可读性的降低,稍稍一经分析便能够读懂。这种稍稍以牺牲可读性来换取效率的做法在STL的实现中比比皆是,本文后面还会有例子。
先从这种惊叹中回过神来,接着看循环的主体部分,其中有一个__median函数,它的作用是取首部、尾部和中部三个元素的中值作为pivot。我们之前学到的快速排序都是选择首部、尾部或者中间位置的元素作为pivot,并不会比较它们的值,在很多情况下这将引起递归的恶化。现在这里采用的中值法可以在绝大部分情形下优于原来的选择。
主循环中另外一个重要的函数是__unguarded_partition,这其实就是我们平常所使用的快速排序主体部分,用于根据pivot将区间分割为两个子序列。其源码如下:
template <class RandomAccessIterator, class T>
RandomAccessIterator __unguarded_partition(RandomAccessIterator first,
RandomAccessIterator last,
T pivot) {
while (true) {
while (*first < pivot) ++first; //first找到 >= pivot的元素就停下来
--last; //因为last 指向的是尾后迭代器,因此要前移一位
while (pivot < *last) --last; //last 找到 <= pivot 的元素就停下来
if (!(first < last)) return first; //两个元素交叉了就说明已经 partition 结束
iter_swap(first, last);
++first; //只需要将 first 后移就行,因为 last 待会儿 --last
}
}它会不断去交换放错位置的元素,直到first和last指针相互交错为止,函数返回的是右边区间的起始位置。注意看:这个函数没有对first和last作边界检查,而是以两个指针交错作为中止条件,节约了比较运算的开支。可以这么做的理由是因为,选择 首 尾 中间 位置三个值的中间值作为pivot,因此一定会在超出此有效区域之前中止指针的移动。《STL源码剖析》给出了两个非常直观的示意图:
分割示例一:
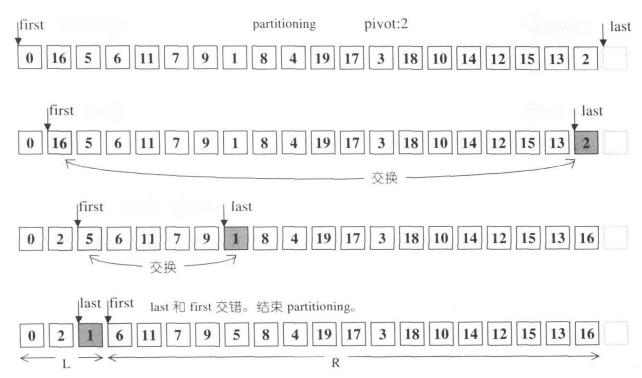
分割示例二:
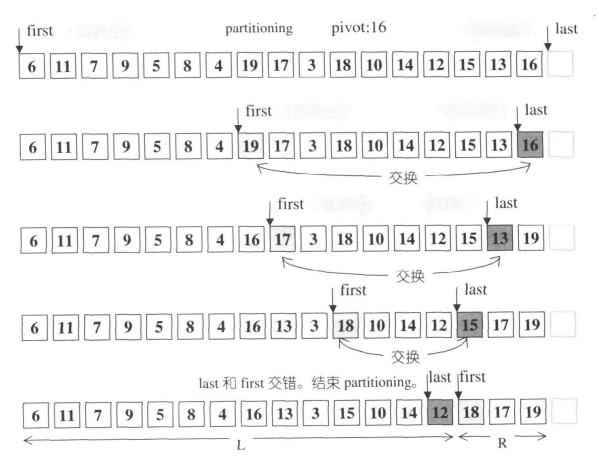
现在我们来关注循环条件和if语句。__introsort_loop的最后一个参数depth_limit是前面所提到的判断分割行为是否有恶化倾向的阈值,即允许递归的深度,调用者传递的值为2logN。注意看if语句,当递归次数超过阈值时,函数调用partial_sort,它便是堆排序:
template <class RandomAccessIterator, class T, class Compare>
void __partial_sort(RandomAccessIterator first, RandomAccessIterator middle,
RandomAccessIterator last, T*, Compare comp) {
make_heap(first, middle, comp);
for (RandomAccessIterator i = middle; i < last; ++i)
if (comp(*i, *first))
__pop_heap(first, middle, i, T(*i), comp, distance_type(first));
sort_heap(first, middle, comp);
}
template <class RandomAccessIterator, class Compare>
inline void partial_sort(RandomAccessIterator first,
RandomAccessIterator middle,
RandomAccessIterator last, Compare comp) {
__partial_sort(first, middle, last, value_type(first), comp);
}如前所述,此时采用堆排序可以将快速排序的效率从O(N2)提升到O(N logN),杜绝了过度递归所带来的开销。堆排序结束之后直接结束当前递归。
除了递归深度阈值以外,Introspective Sort还用到另外一个阈值。注意看__introsort_loop中的while语句,其中有一个变量__stl_threshold,其定义为:
const int __stl_threshold = 16;它就是我们前面所说的最小分段阈值。当数据长度小于该阈值时,再使用递归来排序显然不划算,递归的开销相对来说太大。而此时整个区间内部有多个元素个数少于16的子序列,每个子序列都有相当程度的排序,但又尚未完全排序,过多的递归调用是不可取的。而这种情况刚好插入排序最拿手,它的效率能够达到O(N)。因此这里中止快速排序,sort会接着调用外部的__final_insertion_sort,即插入排序来处理未排序完全的子序列。
到目前为止一切都很好理解。
现在终于来到std::sort的最后一步——插入排序。将它作为单独的一章是因为它使用了些优化技巧,让人难以理解,我花了些时间才弄懂它,这也正是为何会有本文的根本原因。我们先来看看其定义:
template <class RandomAccessIterator>
void __final_insertion_sort(RandomAccessIterator first,
RandomAccessIterator last) {
if (last - first > __stl_threshold) {
__insertion_sort(first, first + __stl_threshold);
__unguarded_insertion_sort(first + __stl_threshold, last);
}
else
__insertion_sort(first, last);
}它被分成了两个分支,前一个分支是处理大于分段阈值的情况,后一个分支处理小于等于分段阈值。第一个问题:为什么要划分成两种情况不同对待?
再看,第一个分支中又将区间分成了两段,前16个和剩余部分,然后分别调用两个排序。于是第二个问题来了,为什么要这么分段?
最后一个问题,__insertion_sort和__unguarded_insertion_sort有何区别?
这此问题便是我看到这个实现的疑惑,为什么不直接使用插入排序?但是很遗憾的是《STL源码剖析》并未讲得很清楚,网上也有类似的讨论,都说是为了优化,但为何这样便能优化,还是没有答案。如果你也无法回答上述三个问题,那么请跟随我一起来讨论。
我们这里先来看最后一个问题,这两种插入排序有何区别?要解释这个问题,需要先介绍它们各自的实现,从标准插入排序算法开始。
插入排序很简单,本文前面的动态图可以很直观的展示它的原理。这里是摘自维基百科的一段伪代码:
for i ← 1 to length(A)
j ← i
while j > 0 and A[j-1] > A[j]
swap A[j] and A[j-1]
j ← j - 1从第二个值开始遍历每个元素,首先判断是否有越界,然后判断是否需要跟前一个元素交换,如果第j个元素小于j-1个元素,那么就交换这两个元素,将j递减,重复执行上述过程,直到到达首部或者前一个元素小于当前元素。
那么同样都是插入排序,__insertion_sort和__unguarded_insertion_sort有何不同,为什么叫unguarded?接下来看看STL的实现:(注:这里取得都是采用默认比较函数的版本)
template <class RandomAccessIterator, class T>
void __unguarded_linear_insert(RandomAccessIterator last, T value) {
RandomAccessIterator next = last;
--next;
while (value < *next) {
*last = *next;
last = next;
--next;
}
*last = value;
}
template <class RandomAccessIterator, class T>
inline void __linear_insert(RandomAccessIterator first,
RandomAccessIterator last, T*) {
T value = *last;
if (value < *first) {
copy_backward(first, last, last + 1);
*first = value;
}
else
__unguarded_linear_insert(last, value);
}
template <class RandomAccessIterator>
void __insertion_sort(RandomAccessIterator first, RandomAccessIterator last) {
if (first == last) return;
for (RandomAccessIterator i = first + 1; i != last; ++i)
__linear_insert(first, i, value_type(first));
}最下面的函数,它是从第二个元素开始对每个元素依次调用了__linear_insert。后者和前面提到的标准插入排序有一点点不同,它会先将该值和第一个元素进行比较,如果比第一个元素还小,那么就直接将前面已经排列好的数据整体向后移动一位,然后将该元素放在起始位置。对于这种情况,和标准插入排序相比,它将last - first - 1次的比较与交换操作变成了一次copy_backward操作,节省了每次移动前的比较操作。
但这还不是最主要的。如果该元素并不小于第一个元素,它会调用另外一个函数__unguarded_linear_insert,这里仅仅挨个判断是否需要调换,找到位置之后就将其插入到适当位置。注意看,这里没有检查是否有越界,为什么可以这样?因为在__linear_insert的if语句中,已经可以确保第一个值(最小的值)在最左边了,如果不在最左边,它便不可能进入这个函数,会执行第一个分支。那么,__unguarded_linear_insert便可以毫无顾忌的省略掉越界的检查。当然,因为少了很多次的比较操作,效率肯定便有了提升。后面我们会就此作一个详细的分析。
注意:使用__unguarded_linear_insert时,一定得确保这个区间的左边有效范围内已经有了最小值,否则没有越界检查将可能带来非常严重的后果。这种unguarded命名的函数在前面__introsort_loop里面也有一个:__unguarded_partition,这也是同样不考虑边界的情况,前面已经介绍过。
最后再来看看__unguarded_insertion_sort在STL中的实现,同样这里只是默认比较函数版本:
template <class RandomAccessIterator, class T>
void __unguarded_insertion_sort_aux(RandomAccessIterator first,
RandomAccessIterator last, T*) {
for (RandomAccessIterator i = first; i != last; ++i)
__unguarded_linear_insert(i, T(*i));
}
template <class RandomAccessIterator>
inline void __unguarded_insertion_sort(RandomAccessIterator first,
RandomAccessIterator last) {
__unguarded_insertion_sort_aux(first, last, value_type(first));
}可以忽略掉这层aux函数的包装,它只是为了获得迭代器所指向的类型,其实这两个函数可以合并为一个。这里直接对每个元素都调用__unguarded_linear_insert,这个函数我们在上节已经分析过,它不对边界作检查。正因为如此,它一定比前面的__insertion_sort要快。
但是有一点需要再次强调一遍:和前面的__unguarded_linear_insert一样,一定得确保这个区间的左边有效范围内已经有了最小值,否则没有越界检查将可能带来非常严重的后果。
接下来我们对以上三种实现的性能作一个分析,这里仅以第i个元素的运算次数作为比较,并不考虑编译器优化,所以只是一个粗略的性能分析。此时前i-1个元素已经排好,假设该第i个元素应该插入的位置离i的平均距离为N。
对于标准插入排序,它需要的操作次数为:
// 标准插入排序伪代码
while j > 0 and A[j-1] > A[j] // 2N次比较运算,N次减法运算
swap A[j] and A[j-1] // N次交换运算(通常理解为3N次赋值运算)
j ← j - 1 // N次自减运算总共为2N次比较,3N次赋值,N次减法,N次自减。
再来看__insertion_sort,因为这里出现了分支,因此需要分开来对待。我们取两种极端情况,先假设每次都是取第一个分支,即value < *first,那么此时N=i:
// __linear_insert函数
if (value < *first) { // 1次比较运算
copy_backward(first, last, last + 1);
// 1次copy_backward
*first = value; // 1次赋值运算
}因为copy_backward最后调用的是memmove,它在C标准库中实现为:
// memmove函数
for (; 0 < n; --n) // N次比较运算,N次自减运算
*sc1++ = *sc2++; // 2N次自增运算,N次赋值运算这里认为自增自减一样,因此总共需要N+1次比较,N+1次赋值,3N次自减。
如果假设每次__insertion_sort都不取第一个分支,即首位的元素已经是最小值,此时:
// __linear_insert函数
if (value < *first) { // 1次比较
// ...
}
else
__unguarded_linear_insert(last, value);
// 见下面
// __unguarded_linear_insert函数
while (value < *next) { // N次比较
*last = *next; // N次赋值
last = next; // N次赋值
--next; // N次自减
}因此总共需要N+1次比较,2N次赋值和N次自减。
再假设两个分支有相同的概率(实际上第二个分支的可能性更大些,在经过__introsort_loop之后的数据更是如此,因为此时最小值已经可以确认位于前16个元素之后,这在后面有证明。因此很快最小值便可以移动到最左端,那么就必然走第二个分支),那么平均所需的操作为:N+0.5次比较,1.5N+0.5次赋值,2N次自减。
由于其直接调用了__unguarded_linear_insert,因而和上述第二个分支类似,但没有了分支判断,所需操作为:N次比较,2N次赋值和N次自减。
在上述基础上再作一点假设,假设每种运算占用CPU的时间一样,那么此时三种算法的结果分别为:
2N + 3N + N + N = 7N
N + 0.5 + 1.5N + 0.5 + 2N = 4.5N + 1
N + 2N + N = 4N假设总共为M个元素,那么平均执行次数为:
7N * M
4.5N * M + M
4N * M可以很明显的看到,后两种的执行次数远远低于第一种,接近标准实现的一半。而最后一种因为少了越界检查,乍看之下似乎无足轻重,但在M非常庞大的情况下,影响相当可观,毕竟这是一个非常根本的算法核心。这也是一直没有省略1的原因。
让我们回到__final_insertion_sort函数,为了唤醒你的记忆,再贴一次它的源代码:
template <class RandomAccessIterator>
void __final_insertion_sort(RandomAccessIterator first,
RandomAccessIterator last) {
if (last - first > __stl_threshold) {
__insertion_sort(first, first + __stl_threshold);
__unguarded_insertion_sort(first + __stl_threshold, last);
}
else
__insertion_sort(first, last);
}此时前面提的最后一个问题:两种插入算法有何区别? 已经有了答案:一个带边界检查而另一个不带,不带边界检查的__unguarded_insertion_sort更快。
那么为什么不直接使用它呢?还记得前面每次介绍它时都有一行加粗的话么?这是因为它有一个前提条件,那便是需要确保最小值已经存在于有效区间的最左边。于是,你可能会想,如果此时可以确定最小值已经位于最左边,那么后面所有的区间内便可以使用最快的__unguarded_insertion_sort算法。没错,STL的设计者也是这么想的。
可是,如何可以确定最小值已经在最左边了呢?或者在一个小的区间内?绝大部分情况下无法确定。但正是由于快速排序的特殊性,可以保证最小值存在于一个小的区域中,接下来我们会证明这一点。
所以他们想到将经过__introsort_loop排序的数据分成两段,假设第一段里面包含了最小值,那么将第一段使用__insertion_sort排序,后一段使用__unguarded_insertion_sort便可以达到效率的最大化。对,STL的设计者们珍爱效率如生命。
到这里,你可以回答第一个问题了:为什么有这样的分支处理?是因为如果数据量足够小,没有必要进行如此复杂的划分,直接一个插入排序便可以搞定。只数据量比较大的情况下,将数据分成两段,前一段使用带边界检查的插入排序,后一段使用不带边界检查的插入排序。
现在最为关键的一个问题来了,如何可以确保前16个元素中一定有最小值?
我们看一下维基百科上快速排序的动画,非常直观:
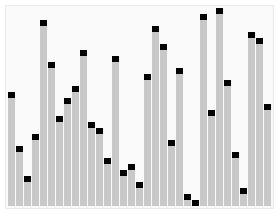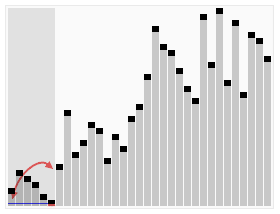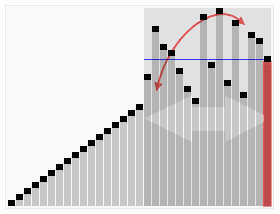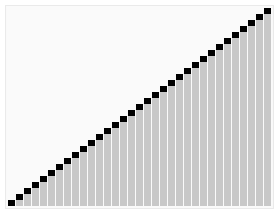
从图中可以看出,无论经过几次递归调用,对于所有划分的区域,左边区间所有的数据一定比右边小,记住这一点,它将为后面的推理起到重要的作用。
再来看一眼__introsort_loop:
template <class RandomAccessIterator, class T, class Size>
void __introsort_loop(RandomAccessIterator first,
RandomAccessIterator last, T*,
Size depth_limit) {
while (last - first > __stl_threshold) {
if (depth_limit == 0) {
partial_sort(first, last, last);
return;
}
--depth_limit;
RandomAccessIterator cut = __unguarded_partition
(first, last, T(__median(*first, *(first + (last - first)/2),
*(last - 1))));
__introsort_loop(cut, last, value_type(first), depth_limit);
last = cut;
}
}该函数只有两种情况下可能返回,一是区域小于等于阈值16;二是超过递归深度阈值。我们现在只考虑最左边的子序列,先假设是由于第一种情况终止了这个函数,那么该子区域小于16。再根据前面的结论:左边区间的所有数据一定比右边小,可以推断出最小值一定在该小于16的子区域内。
假设函数是第二种情况下终止,那么对于最左边的区间,由于递归深度过深,因此该区间会调用堆排序,所以这段区间的最小值一定位于最左端。再加上前面的结论:左边区间所有的数据一定比右边小,那么该区间内最左边的数据一定是整个序列的最小值。
因此,不论是哪种情况,都可以保证起始的16个元素中一定有最小值。如此便能够使用__insertion_sort对前16个元素进行排序,接着用__unguarded_insertion_sort毫无顾忌的在不考虑边界的情况下对剩于的区间进行更快速的排序。
至此,所有三个问题都得到了解答。
这么高效的算法,是不是所有的容器都可以使用呢?我们常规数组是否也能使用?我们知道在STL中的容器可以大致分为:
序列式容器:vector, list, deque
关联式容器:set, map, multiset, multimap
配置器容器(容器适配器):queue, stack, priority_queue
无序关联式容器:unordered_set, unordered_map, unordered_multiset, unordered_multimap。这些是在C++ 11中引入的对于所有的关联式容器如map和set,由于它们底层是用红黑树实现,因此已经具有了自动排序功能,不需要std::sort。至于配置器容器,因为它们对出口和入口做了限制,比如说先进先出,先进后出,因此它们也禁止使用排序功能。
由于std::sort算法内部需要去取中间位置元素的值,为了能够让访问元素更迅速,因此它只接受有随机访问迭代器的容器。对于所有的无序关联式容器而言,它们只有前向迭代器,因而无法调用std::sort。但我认为更为重要的是,从它们名称来看,本身就是无序的,它们底层是用哈希表来实现。它们的作用像是字典,为的是根据key快速访问对应的元素,所以对其排序是没有意义的。
剩下的三种序列式容器中,vector和deque拥有随机访问迭代器,因此它们可以使用std::sort排序。而list只有双向迭代器,所以它无法使用std::sort,但好在它提供了自己的sort成员函数。
另外,我们最常使用的数组其实和vector一样,它的指针本质上就是一种迭代器,而且是随机访问迭代器,因此也可以使用std::sort。
以上便是我所知道的std::sort的所有秘密。仅仅数十行代码,就包含了如此多的技巧,为得只有一个目的:尽最大可能提高算法效率。正如孟岩所说:
STL是精致的软件框架,是为优化效率而无所不用其极的艺术品,是数据结构与算法大师经年累月的智能结晶,是泛型思想的光辉诗篇,是C++高级技术的精彩亮相!
原来只是因为没看明白__final_insertion_sort函数,弄清之后才打算写一篇简短的文章来记录下,所以原来也打算只重点讨论这个函数。可写着写着就发现这个函数脱离不了std::sort,整个std::sort的实现过程中又有着各种各样的考虑,很多的细节在书中、网络上都没有得到解释,如果想要彻底弄明白它的话,需要花费些精力。就如侯捷在《STL源码剖析》一书的自序中所言,这本书的写作动机,纯属偶然。本文也一样,想到既然对这段代码花费了些时间去理解,并从中获益,那我想,应该会有其它人也能从这篇文章中获益吧,那为何不将关于这个算法的所有理解都整理出来呢?于是才有了本文最终的版本。写的过程中颇有感触,自我在脑海中或者笔记上总结,和汇聚成文相比完全是两回事,有太多的背景要介绍,述说的方式,结构的安排等等无一不需花费心思。现在可以体会出每个写作者的艰辛之处,更对认真完成众多经典作品的作者们充满了敬佩。
虽然现在人们认为STL存在非常多的诟病,比如引起代码膨胀、性能下降或者是编译信息难以阅读等,但我认为对于C++而言,它就像C的标准库相对于C语言,可以让我们的工作事半功倍,大大提高工作效率,它是语言不可或缺的部分。毕竟这是C++的标准委员会及众多C++专家们画了数十载的心血,无论是在稳定性、安全性、通用性还是效率上都经历住了很大的考验,如果自己从头开始设计一个自认为更好的库,真的能达到这么好的效果么?看看本文所讨论的std::sort,我实在很难想象还有比STL对它的实现更有效率的做法。当然,如果项目很特殊,比如禁用异常,或者已经有针对项目更高效稳定的量身定制的库,那么我可以理解禁止使用STL。但总的来说,在大部分情况下,有这么好的标准工具,为什么要熟视无睹呢?
标签:
原文地址:http://blog.csdn.net/yapian8/article/details/44061149