蓝桥杯 第39级台阶 DP

标签：

题目描述： 

小明刚刚看完电影《第39级台阶》，离开电影院的时候， 他数了数礼堂前的台阶数，恰好是39级!

    站在台阶前，他突然又想着一个问题：

    如果我每一步只能迈上1个或2个台阶。 先迈左脚，然后左右交替，最后一步是迈右脚， 也就是

说一共要走偶数步。那么，上完39级台阶， 有多少种不同的上法呢？

    请你利用计算机的优势，帮助小明寻找答案。

要求提交的是一个整数。 注意：不要提交解答过程，或其它的辅助说明文字。

基本思路：

将两步合并成一步，就化作了最基本的那种DP

相当于每两步可走2 ，3，4阶台阶，但是需要注意，这里的2,3,4阶台阶都是由两步合并

而来的。因此本身就有集中可能。

记base数组：base【i】表示两步恰好跨过的i阶台阶有几种可能性

                   如：base【1】=0；表示不可能两步恰好跨过1阶台阶

                   base【1】=0，base【2】=1，base【3】=2，base【4】=1；

状态转移方程：F[i]=F[i-1]*base[1]+F[i-2]*base[2]+F[i-3]*base[3]+F[i-4]*base[4];

代码实现：

 1 #include<stdio.h>
 2 
 3 int F[100];//记录偶数步到第i阶台阶的情况数
 4 int base[5]={0,0,1,2,1};//表示两步恰好跨过的i阶台阶有几种可能性
 5 
 6 int main()
 7 {
 8     int i;
 9     F[1]=0;
10     F[2]=1;
11     F[3]=2;
12     F[4]=2;
13 
14     for(i=5;i<=40;i++)
15         F[i]=F[i-1]*base[1]+F[i-2]*base[2]+F[i-3]*base[3]+F[i-4]*base[4];
16 
17     printf("%d\n",F[39]);
18 
19     return 0;
20 }

运行结果：
          

蓝桥杯 第39级台阶 DP

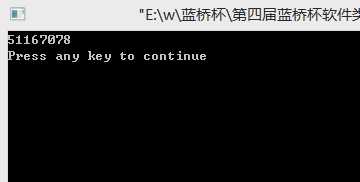
标签：

原文地址：http://www.cnblogs.com/yanglingwell/p/4315152.html