标签:
Reference:http://ufldl.stanford.edu/wiki/index.php/Softmax_regression
起源:Logistic的二类分类
Softmax回归是Logistic回归的泛化版本,用于解决线性多类(K类)的分类问题。Logistic回归可以看作是Softmax回归在K=2时的特例。
①如何从2类转化为K类?
解决方案是引入K组(W、b)参数,选择$max P(Y=j|x^{i},\theta,b)$作为最终分类即可。
由于存在K组参数,原来的$h(\theta)=sigmoid(Inner)$将从单个值,变成一个大小为K的向量。
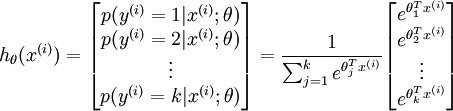
②变化的目标函数
Logistic的目标函数: $J(\theta)=\sum_{i=1}^{m}(1-y^{(i)})log(1-h_{\theta}(x^{i})+y^{i}log(h_{\theta}(x^{(i)}))$
在Softmax里,由于h_{\theta}(x^{(i)}已经变成了向量,所以不能再使用。
实际上,在Logistic的推导里,h_{\theta}(x^{(i)}只是偶然而已,$P(y=0|x;\theta)=h(\theta)$。
即$P(y|x;\theta)$才是真正的概率密度函数。由于y的取值变成的K类,所以新的概率密度函数表示如下:
$P(y^{(i)}=j|x;\theta)=\frac{e^{W_{j}X^{i}}}{\sum_{l=1}^{k}e^{W_{l}X^{i}}}$
且定义$1\{y_{i}=j\}=(y_{i}==j)?1:0$
则 $J(\theta)=\sum_{i=1}^{m}\sum_{j=0}^{l}1\{y_{i}=j\}log\frac{e^{W_{j}X^{i}}}{\sum_{l=1}^{k}e^{W_{l}X^{i}}}$
仔细观察,其实就是$h_{\theta}(x^{(i)})$这个向量根据$y^{(i)}$情况抽取的单个值而已。
梯度变成:$\frac{\partial J(\theta)}{\partial \theta}=\sum_{i=1}^{m}\sum_{l=1}^{k}x^{(i)}(1\{y_{i}=j\}-P(y^{(i)}=j|x;\theta))$
标签:
原文地址:http://www.cnblogs.com/neopenx/p/4316611.html