图的基本概念

标签：

　　图是一种比树结构更复杂的数据结构。在图中一个节点的前驱节点和后继节点的数目是没有限制的，任意两个节点之间都可能有直接的关系。

　　图的定义：图G是由集合V和E构成的二元组，记作G=(V,E)，其中V是图中顶点的非空有限集合，E是图中边的有限集合。从数据结构的逻辑关系角度来看，图中任一顶点都有可能与其它顶点有关系，而图中所有顶点都有可能与某一顶点有关系。在图中，数据结构中的数据元素用顶点表示，数据元素之间的关系用边表示。

　　① 有向图。若图中每条边都是有方向的，那么顶点之间的关系用<v_i,v_j>表示，他说明从v_i到v_j有一条有向边（也称为弧）。v_i是有向边的起点，称为弧尾；v_j是有向边的终点，称为弧头。所有边都有方向的图称为有向图。

　　② 无向图。若图中的每条边都是无方向的，顶点v_i和v_j之间的边用(v_i,v_j)表示。因此，在有向图中<v_i,v_j>与<v_j,v_i>分别表示两条边，而在无向图中(v_i,v_j)与(v_j,v_i)表示的是同一条边。

　　③ 完全图。若一个无向图中具有n个顶点，而每一个顶点与其它n-1个顶点之间都有边，则称之为无向完全图。显然，含有n个顶点的无向完全图共有n(n-1)/2条边。类似地，有n个顶点的有向完全图中边的数目为n(n-1)，即任意两个不同顶点之间都有方向相反的两条边存在。

　　④ 度、出度和入度。顶点v的度是指关联于该顶点的边的数目，记作D(v)。若G为有向图，顶点的度表示该顶点的入度和出度之和。顶点的入度是以该顶点为终点的有向边的数目，而顶点的出度是指以该顶点为起点的有向边的数目之和，分别记为ID(v)和OD(v)。

　　⑤ 路径。在图G中，两个顶点之间的路径长度是指路径上经过的边的数目。第一个顶点和最后一个顶点相同的路径称为回路或环。若一条路径上只有始、末顶点相同以外，其余顶点均不相同，则称其为简单路径。

　　⑥ 子图。若有两个图，G=(V,E)和G1=(V1,E1)，如果V1包含于V，且E1包含于E，则称G1为G的子图。

　　⑦ 连通图与联通分量。在无向图G中，若从顶点v1到顶点v2有路径，则称顶点v1和顶点v2是连通的。如果无向图G中任意两个顶点都是连通的，则称其为连通图。无向图G的极大连通子图称为G的连通分量。

　　⑧ 强连通图与强连通分量。在有向图G中，如果对于每一对定点v1,v2属于V且v1不等于v2，从顶点v1到顶点v2和从顶点v2到顶点v1都存在路径，则称图G为强连通图。有向图中的极大连通子图称为有向图的强连通分量。

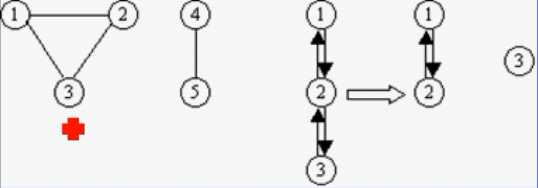
　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　左右分离的两部分子图称为连通分量

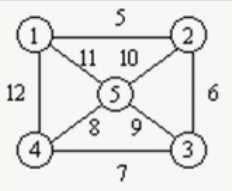
　　⑨ 网。边（或弧）带权值的图称为网。

　　⑩ 有向树。如果一个有向图恰有一个顶点的入度为0，其余顶点的入度均为1，则是一棵有向树。

图的基本概念

标签：

原文地址：http://www.cnblogs.com/ImaY/p/4312877.html