标签:
这一节讲述的是机器学习的核心、根本性问题——学习的可行性。学过机器学习的我们都知道,要衡量一个机器学习算法是否具有学习能力,看的不是这个模型在已有的训练数据集上的表现如何,而是这个模型在训练数据外的数据(一般我们称为测试数据)上性能的好坏,我们把这个性能称为泛化能力(generalization ability),机器学习中,我们的目标是寻找高泛化能力的模型;有些模型虽然在训练数据集上分类效果很好,甚至正确率达到100%,但是在测试数据集上效果很差,这样的模型泛化能力很差,这种现象也叫过拟合(Overfitting)。
如果我们能够获取测试数据,我们就可以据此估计一个模型的泛化能力了。可问题是,很多时候,我们只有一个训练集,而额外再获取sample是十分困难的事,例如医学上为一个病人做临床诊断都需要花费大量人力和财力。关于如何估计一个模型的泛化能力,这个我以后 会讲, 而这一节 我主要想讨论一个更有意思的问题,我们能否利用训练误差来估计泛化误差?
这里,我们把训练误差称作in sample error,即样本内误差,记为$E_{in}=\frac{1}{N}\sum_{i=1}^N I[h(x)\neq f(x)]$,其中$N$为训练集样本数,$h(x)$为假设,$f(x)$为target function。
样本外误差称作out sample error,定义为$E_{out}=E_{x\sim P}[I( h(x)\neq f(x))]$
样本外误差其实就是我们常说的期望损失
机器学习问题中,目标函数$f$和分布$P$一般都是未知的,也就是说,只给定训练数据集的前提条件下,$E_{out}$我们没法知道(除非加上一些假设)。那么在没办法知道样本外误差的情况下,我们如何选择一个模型呢?最容易想到的办法自然是 从假设集中挑选出训练误差小的假设, 直观上这很容易理解, 在训练数据集上表现好的模型,在训练集外的数据也应该表现好,可真的如此吗?答案是否。
我们先来看一个例子,然后再把学习问题与这个问题进行类比。
假设我们有一个罐子,罐子里装着很多橘色或者绿色的弹珠,如果我们想知道橘色珠子的比例是多少(记为$\mu$),该如何做?
当然你会说 ,这还不简单,一个一个数过去不就清楚了吗?但问题是,如果这个罐子很大,比如有1万个弹珠,你还会一个一个去数吗?显然是不可行的。学过统计的我们都知道还有一个办法,那就是抽样(sampling)。比如抽出10个弹珠,然后计算这个样本中橘色弹珠的比例(记为$\nu$)来作为整个罐子中橘色弹珠比例的估计。那么$\nu$是否告诉我们关于$\mu$一些有用信息?
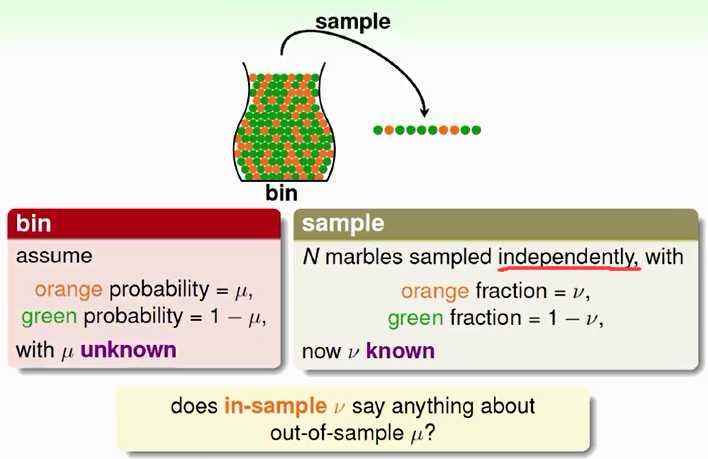
首先,$\mu$一定等于$\nu$吗? 不一定,因为我们有可能抓起一把弹珠,而这把弹珠全部都是绿的。不过我们有很大把握说$\nu$是和$\mu$很接近的。数学上,刻画$\mu$和$\nu$有多接近,是由一个著名的不等式来规范的,这个不等式称为Hoeffding‘s inequality。

式中,$\epsilon$是一个误差限,$N$是样本大小。Hoeffding不等式告诉了我们这样一个事实:当样本集越大时,$\nu$和$\mu$相差很大的概率越小。也就是说,$\nu=\mu$这件事大概是对的,因为随着样本的增大,这个概率的上限将会越来越小;差不多是对的,因为我们可以缩小让$\nu$和$\mu$很接近。数学上,我们把这个性质称作PAC(probably approximately correct,可能近似正确)。如果N很大,我们就可以用$\nu$来估计$\mu$。

介绍完Hoeffding不等式,让我们看看这个问题与学习问题的联系。
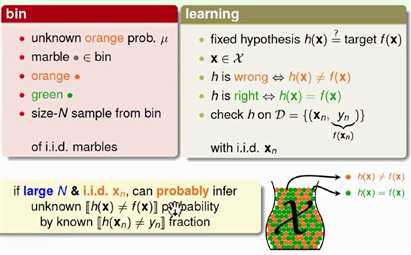
球罐模型中,我们不知道的是橘色弹珠的比例,而对应到学习问题中我们想知道的是总体上一个假设和目标函数是否接近。样本空间中的每一个样本点$x\in\mathcal{X}$对应于球罐中的每一个弹珠,当假设h(x)和f(x)不一样时,我们就把球漆成橘色;一样时,我们就把球漆成绿色。从球罐中抽取的石子儿对应到学习问题中的训练集D,同样是iid采样的。球罐模型的目的是用抽样计算出的比例估计真实的比例,而学习问题中我们的目的是用in sample error估计out sample error。
做了此番类比,于是我们就能套用Hoeffding不等式得出类似的结论:

对于一个固定的h来说,如果N很大,那么Ein和Eout相差很大的概率就很小,也就是二者很接近。同样,这条不等式的成立与$\epsilon,N,E_{out}$无关,Ein=Eout是PAC的。如果Ein很小,且$E_{in}\approx E_{out}$,那么我们有很大的把握说 Eout也很小,从而得出h与f很相似(专业一点来说,就是$h=f$ 是PAC的)。同理,如果Ein很大,那么Eout也可能很大,那么我们就说$h\neq f$是PAC的。但也有一个例外情况,Ein很小,Eout很大,也就是常说的过拟合。
PRML里面提到,增大样本数能够减小过拟合现象,以前一直没有搞懂原因,如今学了Hoeffding不等式和PAC框架有点明白了。增大样本数N,能够缩小Hoeffding不等式右侧概率的上限,提高了in sample error与out sample error接近的概率,从而我们用得到的in sample error对out sample error估计的时候更加准确。
标签:
原文地址:http://www.cnblogs.com/wacc/p/4314424.html