标签:
起源:线性神经网络与单层感知器
古老的线性神经网络,使用的是单层Rosenblatt感知器。该感知器模型已经不再使用,但是你可以看到它的改良版:Logistic回归。
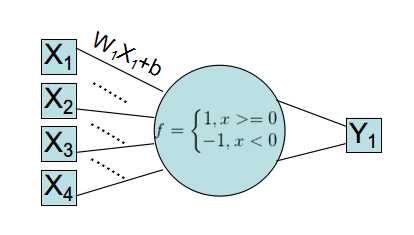
可以看到这个网络,输入->加权->映射->计算分类误差->迭代修改W、b,其实和数学上的回归拟合别无二致。
其中迭代修改参数,使目标函数收敛这一数学过程,被某些神经科学家脑补成大脑神经元的工作过程。于是各种高大上的神经网络就开始乱吹了。
Logistic对该模型进行了改良:
①Rosenblatt感知器使用的是sgn函数作为加权映射到输入层的方式,该函数其实不是很平滑,区分特征效果不好。
于是Logistic回归里,改换成了Logistic-Sigmoid函数。(Sigmoid函数被认为是映射区分特征的神器,也是BP网络非线性分类的核心)
②使用了基于概率论-最大似然估计的方法设计误差目标函数。
线性神经网络使用的LMS(最小均方)的数学原理其实可由最大似然估计+假设误差概率模型得到。(详见Andrew Ng视频)
似然函数的数值范围要大于LMS,尤其是二类情况下,LMS的数值范围比较小。
实际上,这两种模型的起源都是最小二乘法的线性回归。不同的是,早期的解决线性回归使用的矩阵求解(牛顿法)。
梯度迭代使目标函数收敛的数学方法,可以看作是神经网络的起源。
Part I :BP网络的结构与工作方式
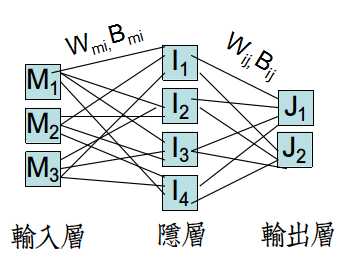
BP网络中使用隐层(HideLayer)设定,目的是通过全连接的网络+Sigmoid函数,疯狂地参数加权、映射来区分特征。
从数学上是很难解释原理的。(与之相对的是SVM支持向量机,最大化间隔数学原理让你竟无言以对)。
隐层层数和每层的神经元个数决定着网络复杂度,已有数据表明(单、双隐层), 每层神经元个数与样本个数相近,网络效率最高。
BP网络的工作方式分为两部分:
①FP(Front Propagation)前向传播:输入->线性加权传至隐层->在隐层Sigmoid并输出->线性加权传至输入层
->输入层使用Sigmoid(或线性函数)处理输入,进行分类,计算误差并累加到总误差(目标函数)
②BP(Back Propagation) 反向传播:从输入层开始,由当前处理单条数据的误差,通过梯度法更新Wij、Bij。
由于网络的特殊性,此时Wmi、Bmi的更新依赖于Wij、Bij,只能反向更新。
BP网络训练数据有两种方法:
①单样本串行:按顺序输入每个样本,对每个样本执行FP、BP,累计总误差。
执行完毕之后,算一次迭代,继续从第一个样本开始,进行第二次迭代。直至总误差收敛,退出迭代。
②批样本并行:(留坑,不会手艹代码)
Part II:BP过程的公式推导
定义ui,vi,uj,vj,分别是隐层、输入层的I/O。
Sigmoid函数的导数:$S^{‘}(x)=S(x)(1-S(x))$
标签:
原文地址:http://www.cnblogs.com/neopenx/p/4321797.html