标签:
首先是从二叉搜索树开始,一棵二叉搜索树的定义是:
1.这是一棵二叉树;
2.令x为二叉树中某个结点上表示的值,那么其左子树上所有结点的值都要不大于x,其右子树上所有结点的值都要不小于x。
由二叉搜索树的第二条定义,可以很方便地利用这种特点在二叉树中以O(logn)的渐进复杂度完成插入、查找、删除等操作。
但是这里还是有个问题,就是弄不好的话,一棵普通的二叉搜索树经过多次修改操作之后可能会导致整棵树左右“不平衡”,出现一边结点很多,另一边结点很少的情况,这样最终每一次的操作时间就会大大偏离O(logn),甚至最后退化成一条链。
平衡树就是通过一系列的操作,不断动态维持二叉搜索树的左右平衡,始终保证二叉搜索树的效率。
SBT全称Size Balanced Tree,是一种通过记录以每个结点为根的子树中的结点的个数size,然后进行二叉搜索树结构调整的方法,由OI选手陈启峰发明。
SBT除了一般的二叉搜索树性质之外,还有两条性质:
对于SBT中的每一个结点t,有:
1.s[right[t]]>=s[left[left[t]]],s[right[left[t]]];
2.s[left[t]]>=s[left[right[t]]],s[right[right[t]]].
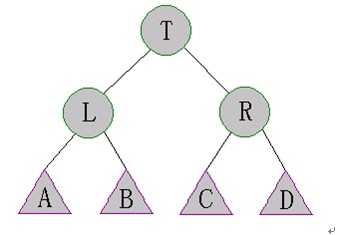
即在上图中:
s[L]>=s[C],s[D];s[R]>=s[A],s[B].
这一性质能够保证整棵SBT能够在整体的结构上保持相对平衡,而为了保持这一额外的性质,需要通过不断的调整来完成。
调整即通过结点的左右旋完成,左右旋不改变二叉搜索树的性质,而能够调整SBT的size,使得整棵树能够始终保持为一棵SBT树。
这是SBT的核心操作,保持过程通过左右旋来完成。
与普通的二叉搜索树相同,只是在插入完之后加入一个maintain操作。
与普通的二叉搜索树相同。删除完一个结点之后虽然不能够保证此时的树还能够严格保持SBT性质,但是树结构从整体上来说最大深度不会增加,因此maintain操作就不需要进行了。
与普通的二叉搜索树相同。
由于size的存在,SBT天生就很适合处理查找第k个数这样的任务。不断确定一下左子树和右子树的size即可,若某结点左子树的size+1=k,那么该结点就是第k个数。
与普通的二叉搜索树相同。
与普通的二叉搜索树相同。
代码
标签:
原文地址:http://www.cnblogs.com/jcf94/p/4323571.html