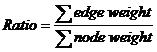
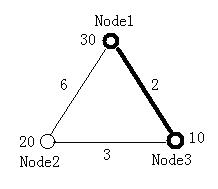
3 2 30 20 10 0 6 2 6 0 3 2 3 0 2 2 1 1 0 2 2 0 0 0
1 3 1 2
#include<stdio.h>
const int N = 20;
const int inf = 9999999;
int nodew[N],map[N][N],n,m;
int prim(int sta,int s)
{
int ins[N]={0},node[N],ts,mint,k=m,sum;
k--; ins[s]=1; sum=0;
for(int i=0;i<=n;i++)
node[i]=inf;
node[s]=0;
while(k)
{
mint=inf;
for(int i=0;i<n;i++)
if(!ins[i]&&((1<<i)&sta))
{
if(node[i]>map[s][i])
node[i]=map[s][i];
if(node[i]<mint)
mint=node[i],ts=i;
}
if(mint!=inf)
{
s=ts; sum+=mint; ins[s]=1; k--;
}
else break;
}
if(k)
return -1;
else return sum;
}
int main()
{
int sum_e=inf,sta;
double sum_n;
while(scanf("%d%d",&n,&m)>0&&n+m!=0)
{
for(int i=0;i<n;i++)
scanf("%d",&nodew[i]);
for(int i=0;i<n;i++)
for(int j=0;j<n;j++)
scanf("%d",&map[i][j]);
sum_e=inf; sum_n=1;
for(int s=1;s<(1<<n);s++)
{
int k=0,id,tsum_e;
double tsum_n=0;
for(int i=0;i<n;i++)
if(s&(1<<i))
tsum_n+=nodew[i],k++,id=i;
if(k!=m)continue;
tsum_e=prim(s,id);
if(tsum_e!=-1)
if(tsum_e/tsum_n<sum_e/sum_n)
sum_e=tsum_e,sum_n=tsum_n,sta=s;
}
int i;
for(i=0; i<n; i++)
if((1<<i)&sta)
{
printf("%d",i+1); break;
}
for(i++ ; i<n; i++)
if((1<<i)&sta)
printf(" %d",i+1);
printf("\n");
}
}
HDU2489Minimal Ratio Tree(最小生成树+状态压缩)
原文地址:http://blog.csdn.net/u010372095/article/details/44178969