标签:
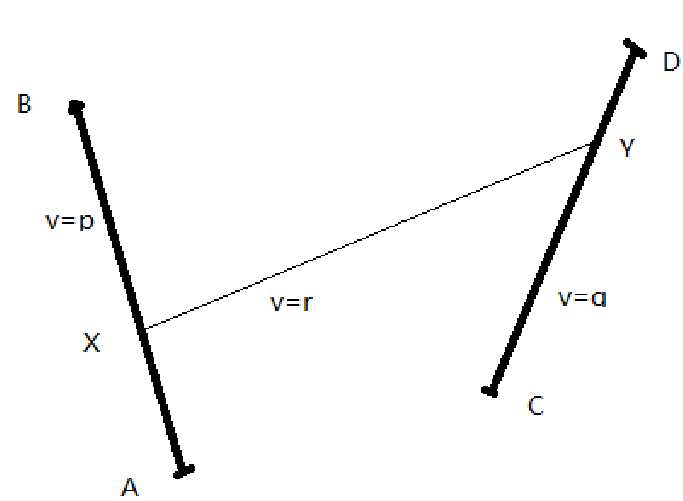
这道题是一道3分搜索的题。其实这种题很多时候都出现在高中的解析几何上,思路很简单,从图中可以看到,肯定在AB线段和CD线段上各存在一点x和y使得所花时间最少
因为AB和CD上的时间与x和y点的坐标都存在一个凸函数的关系,所以可以想到利用3分搜索的方式进行求解。当然这里要用到两个三分搜索的嵌套,锁定x后找到满足条件的y,知道最小的满足条件的x和y。用三分搜索的好处就是
可以利用两点的中点坐标公式,这样比用存数学公式求解要方便的多。

#include"iostream" #include"stdio.h" #include"algorithm" #include"string.h" #include"cmath" #define mx 1005 #define exp 1e-6 using namespace std; double p,q,r; struct point { double x,y; }; double dist(point a,point b) { return sqrt((a.x-b.x)*(a.x-b.x)+(a.y-b.y)*(a.y-b.y)); } double find2(point x,point c,point d) { point left,right,mid,midmid; double t1,t2; left=c; right=d; do { mid.x=(left.x+right.x)/2; mid.y=(left.y+right.y)/2; midmid.x=(mid.x+right.x)/2; midmid.y=(mid.y+right.y)/2; t1=dist(x,mid)/r+dist(mid,d)/q; t2=dist(x,midmid)/r+dist(midmid,d)/q; if(t1>t2) left=mid; else right=midmid; }while(abs(t1-t2)>exp); return t1; } double find1(point a,point b,point c,point d) { point left,right,mid,midmid; double t1,t2; left=a; right=b; do //先循环,这样可以不用给t1,t2赋初值 { mid.x=(left.x+right.x)/2; mid.y=(left.y+right.y)/2; midmid.x=(mid.x+right.x)/2; midmid.y=(mid.y+right.y)/2; t1=dist(a,mid)/p+find2(mid,c,d); t2=dist(a,midmid)/p+find2(midmid,c,d); if(t1>t2) left=mid; else right=midmid; }while(abs(t1-t2)>exp); return t1; } int main() { int t; cin>>t; point a,b,c,d; while(t--) { cin>>a.x>>a.y>>b.x>>b.y>>c.x>>c.y>>d.x>>d.y; cin>>p>>q>>r; printf("%.2lf\n",find1(a,b,c,d)); } return 0; }
标签:
原文地址:http://www.cnblogs.com/acm-jing/p/4326826.html