标签:
最大子矩阵和问题以POJ1050为例:给出一个矩阵,找出该矩阵的最大子矩阵和
例如:
0 -2 -7 0
9 2 -6 2
-4 1 -4 1
-1 8 0 -2
最大子矩阵为:
9 2
-4 1
-1 8
and has a sum of 15.
分析:首先,我们考虑一种极端的方法,如果这个数组a是一个一维数组,那么这个问题就转换成为了最大子段和问题:最大子段和b[i]=max(b[i-1]+a[i],a[i]),b[i]指的是0到i的最大子段和。
#include <cstdio> int max_sum=-0xffff; int a[10000]={0}; int main() { int n; scanf ("%d",&n); for(int i=1;i<=n;i++) { scanf ("%d",&a[i]); if(a[i-1]>0) a[i]=a[i]+a[i-1]; if(a[i]>max_sum) max_sum=a[i]; printf("%d ",a[i]); } printf("\n%d",max_sum); }
那么,我们会想,如何才能把二维数组问题转换成为一维数组问题呢?
好了,现在我们来看二维数组情况,对于一个二维数组,和最大子矩阵有很多种情况,这个子矩阵可能有1,2,3.。。各种情况,这样,我们就需要枚举所有情况之下的子矩阵和,然后找出这个最大的。
1 scanf ("%d",&n);
2 for(i=1;i<=n;i++)
3 for(j=1;j<=n;j++)
4 {
5 scanf ("%d",&a[i][j]);
6 a[i][j]+=a[i-1][j]; //第二行的数是第一行与第二行的和,如此,第三行的数值即为第二行与输入的第三行的和,那么就是说,后一行的数值都是前面所有行数的累加和
7 }
8 for(i=1;i<=n;i++)
9 {
10 for(j=1;j<=n;j++)
11 printf("%d ",a[i][j]);
12 printf("\n");
13 }
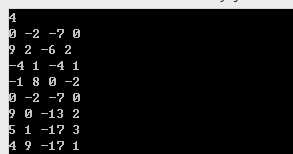
如上图所示。
然后我们需要求最大子矩阵和。看如下代码:
int max=a[1][1];//需要一个记录最大子矩阵和
for(i=0;i<=n-1;i++)//在这里,j-i遍历的就是子矩阵行数的所有情况。
{
for(j=i+1;j<=n;j++)
{
int b[1000];//需要一个中间数组来记录当子矩阵行数确定之后,我们还需要找出这些列数不同的子矩阵中和最大的那个。
memset(b,0,sizeof(b));//先把b数组置0
for(k=1;k<=n;k++)子矩阵的列数从1列举到n
{
if(b[k-1]>=0)//如果观察仔细的话,我们可以发现,这里的运算方式其实和上面求最大子段和的方法是一样的。
//如果b[k-1]所记录的子矩阵和大于等于的话,那么就是b[k]=b[k-1]+a[j][k]-a[i][k].
b[k]=b[k-1]+a[j][k]-a[i][k];
else
b[k]=a[j][k]-a[i][k]; //否则,b[k]=b[k]=a[j][k]-a[i][k]
if(b[k]>max)
max=b[k];
}
}
}
printf("%d",max);
这其实就把所有子矩阵都遍历了一遍,然后挑选出最大的值。
完整代码:
#include <cstdio>
#include <cstring>
int a[1000][1000];
int n;
int main()
{
int i,j,k;
scanf ("%d",&n);
for(i=1;i<=n;i++)
for(j=1;j<=n;j++)
{
scanf ("%d",&a[i][j]);
a[i][j]+=a[i-1][j];
}
for(i=1;i<=n;i++)
{
for(j=1;j<=n;j++)
printf("%d ",a[i][j]);
printf("\n");
}
int max=a[1][1];
for(i=0;i<=n-1;i++)
{
for(j=i+1;j<=n;j++)
{
int b[1000];
memset(b,0,sizeof(b));
for(k=1;k<=n;k++)
{
if(b[k-1]>=0)
b[k]=b[k-1]+a[j][k]-a[i][k];
else
b[k]=a[j][k]-a[i][k];
if(b[k]>max)
max=b[k];
}
}
}
printf("%d",max);
return 0;
}
感谢beiyeqingteng对我的启发。
标签:
原文地址:http://www.cnblogs.com/bei-insomia/p/4328835.html