标签:
https://leetcode.com/problems/set-matrix-zeroes/
Given a m x n matrix, if an element is 0, set its entire row and column to 0. Do it in place.
Did you use extra space?
A straight forward solution using O(mn) space is probably a bad idea.
A simple improvement uses O(m + n) space, but still not the best solution.
Could you devise a constant space solution?
解题思路:
这道题看似简单,不知道要考什么。细细思考后,难度主要在于两点。
第一,不能遇到0就立刻将该行该列的所有元素都置为0,因为原来数组中就有0,该行该列可能本来就有0。这样无法判断到底是本来就是0,还是后来置为0的。
第二,如何用常数的空间来做。我们可以用一个set记录原来就是0的行号和列号,但需要m+n的空间。
下面先实现m+n的。
public class Solution { public void setZeroes(int[][] matrix) { Set<Integer> rowSet = new HashSet<Integer>(); Set<Integer> columnSet = new HashSet<Integer>(); for(int i = 0; i < matrix.length; i++){ for(int j = 0; j < matrix[0].length; j++){ if(matrix[i][j] == 0){ columnSet.add(j); rowSet.add(i); } } } for(int i = 0; i < matrix.length; i++){ for(int j = 0; j < matrix[0].length; j++){ if(columnSet.contains(j)){ for(int k = 0; k < matrix.length; k++){ matrix[k][j] = 0; } } if(rowSet.contains(i)){ for(int k = 0; k < matrix[0].length; k++){ matrix[i][k] = 0; } } } } } }
下面思考如何在常数空间内实现,百思不得其解,考虑人脑是如何做的。
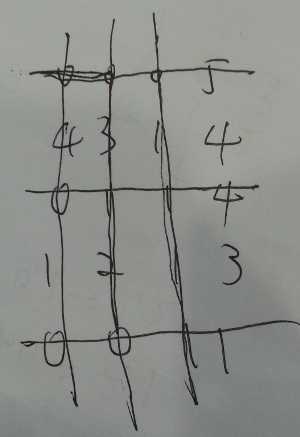
遇到0就用线将他们连起来,而不能直接置为0,不然无法区分是不是原来就是0。然后再将所有的线置为0。这个过程不用额外空间,但是需要将元素临时置为一个不是integer的符号,以免与原来的元素冲突,这在所有元素都是integer的数组里做不到。
只能看看别人是怎么做的。思路如下。
借用每列的第一行和每行的第一列来存储当前列和当前行是不是有0,如果有0,就把当前行的第一列和当前列的第一行置为0,反正本来这里最后一定是0。
于是问题来了,最后处理第一行和第一列的标志位时,如何知道这里是作为标志的0,还是原来就为0?比如,如果原来matrx[1][0]就是0,那么这时第一列就要全部置为0,但如果matrx[1][0]是作为标志位的0,第一列是不能被全部置为0的,否则导致的结果是最后matrix所有元素都是0了。列的标志位(即第一行)也是同样的道理。
这里遇到的问题和上面的问题一样,就是如何区分标志位和原来的值。我们这里用另一个思路来解决。
最后借助标志位赋值时,只将从第二行和第二列开始的元素置为0。第一行和第一列是否置为0,不用标志位来看,借助另外两个变量firstColumnHasZero和firstRowHasZero,这两个变量在前面遍历matrix的时候另外存储。
public class Solution { public void setZeroes(int[][] matrix) { boolean firstColumnHasZero = false; boolean firstRowHasZero = false; for(int i = 0; i < matrix.length; i++){ for(int j = 0; j < matrix[0].length; j++){ if(matrix[i][j] == 0){ if(j == 0){ firstColumnHasZero = true; }else{ matrix[0][j] = 0; matrix[i][0] = 0; } if(i == 0){ firstRowHasZero = true; }else{ matrix[0][j] = 0; matrix[i][0] = 0; } } } } //处理列 for(int i = 1; i < matrix[0].length; i++){ if(matrix[0][i] == 0){ for(int k = 0; k < matrix.length; k++){ matrix[k][i] = 0; } } } //处理行 for(int i = 1; i < matrix.length; i++){ if(matrix[i][0] == 0){ for(int k = 0; k < matrix[0].length; k++){ matrix[i][k] = 0; } } } if(firstRowHasZero){ for(int k = 0; k < matrix[0].length; k++){ matrix[0][k] = 0; } } if(firstColumnHasZero){ for(int k = 0; k < matrix.length; k++){ matrix[k][0] = 0; } } } }
这道题要考的是,尽可能的缩减程序所需的空间。不过我感觉实用性不大,因为思路还是比较复杂的。但是有一点,就是知道思路后如何写出bug free的code。因为这段代码中循环很多,相应的边界值也很关键。能写出,或者一次性写出很好的代码,还是不太容易的。
标签:
原文地址:http://www.cnblogs.com/NickyYe/p/4329225.html