标签:
---恢复内容开始---
使用complex类来写计算几何。
第一题 传送门:
题意给定一直线输入一个点求输入点到该直线射影交点的坐标:
=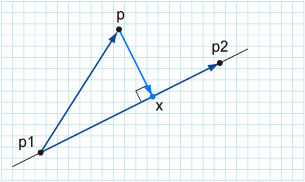
p0到p2向量称为v2,p0到p1向量称为v1 易求得p0到t的向量为 (v2·v1)*(v1的方向向量) 。
用复数表示每个点和每个向量,则将v1*(v2的共轭复数)得到的实部就是x1*x2虚部就是y1*y2。
这样求得了p0到t的向量v3,所以ansx=xp0+xv3,ansy=yp0+yv3;
第二题 题意类似,做法相同。不再赘述。
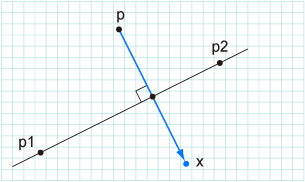
现在贴第二题代码供参考
#include <iostream> #include <cstdio> #include <complex> using namespace std; typedef complex <double> Point; typedef complex <double> Vector; Point p1,p2,p3; Vector v1,v2,v3,v4; int main() { double x1,y1,x2,y2; scanf("%lf%lf%lf%lf",&x1,&y1,&x2,&y2); p1=Point(x1,y1); p2=Point(x2,y2); v1=Vector((x2-x1),(y2-y1)); int n; scanf("%d",&n); while(n--){ double a,b; scanf("%lf%lf",&a,&b); p3=Point(a,b); v2=Vector(a-x1,b-y1); v3=(conj(v1)*v2).real()*v1/norm(v1); //conj求共轭复数 double ansx=v3.real()+x1,ansy=v3.imag()+y1; v4=Vector(2*(ansx-a),2*(ansy-b)); double aansx=v4.real()+a,aansy=v4.imag()+b; printf("%.10lf %.10lf\n",aansx,aansy); } return 0; }
---恢复内容结束---
计算几何入门之aizu两题 Projection Reflection
标签:
原文地址:http://www.cnblogs.com/Scale-the-heights/p/4334123.html