opengl ES中的透视

标签：

由于正交投影的局限性，他只能保证适应屏幕宽高比，但是无法在一定范围内创建出将三维效果转换为二维效果，因此我们使用在绘画艺术中使用的一种技巧：

（关于透视方法下面有个网站介绍的不错，配图也很容易懂：http://www.artyfactory.com/index.html ）

因为我们去掉了正交投影，准备使用透视投影，因此有必须要说明透视投影的一些特征。

透视投影有一个名为视锥体的特殊名词，这个的简介有一位博主的介绍相当不错：

http://www.cnblogs.com/graphics/archive/2012/07/25/2582119.html

这个博文里面也有讲透视，建议读者看一下，肯定比我讲得好。

简而言之，视锥体式通过一个矩阵构造一个类金字塔型的虚拟空间，其他部分是不可见的，这个空间被映射到设备上被转化为二位坐标，为了使得其产生三维效果，就定义了一个透视方法来转化，类似这样：

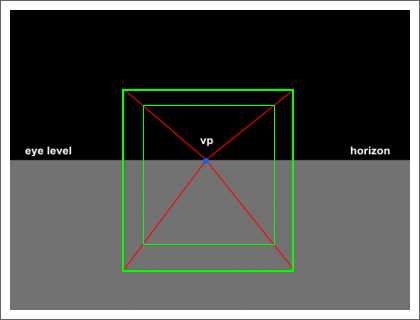
vp就是视锥体的顶点，那个小的方形是近端，大的是远端，绘画的效果产生后：

可以看出这样就产生了三维效果。

透视投影矩阵的产生可以参考Android自带的opengl中的矩阵源码，但是要android4.x以上，因此建议参考源码自己实现，下面是书中给的实现：

 1 public static void perspectiveM(float[] m,float yFovInDegree,float aspect,float n,float f){
 2         final float angleInRadians = (float)(yFovInDegree * Math.PI /180.0);
 3         final float a=(float)(1.0/Math.tan(angleInRadians/2.0));
 4 
 5         m[0] = a/aspect;
 6         m[5] = a;
 7         m[10] = -((f+n)/(f-n));
 8         m[11] = -1f;
 9         m[14] = -((2f*f*n)/(f-n));
10 
11         m[1]=0f;
12         m[2]=0f;
13         m[3]=0f;
14         m[4]=0f;
15         m[6]=0f;
16         m[7]=0f;
17         m[8]=0f;
18         m[9]=0f;
19         m[12]=0f;
20         m[13]=0f;
21         m[15]=0f;
22     }

这仅仅是一个简单的透视矩阵的实现，远近范围在-1~-10之间，观察顶点在屏幕之外，就是不是在屏幕内部。

通过加入一个立方体旋转来查看透视的效果：

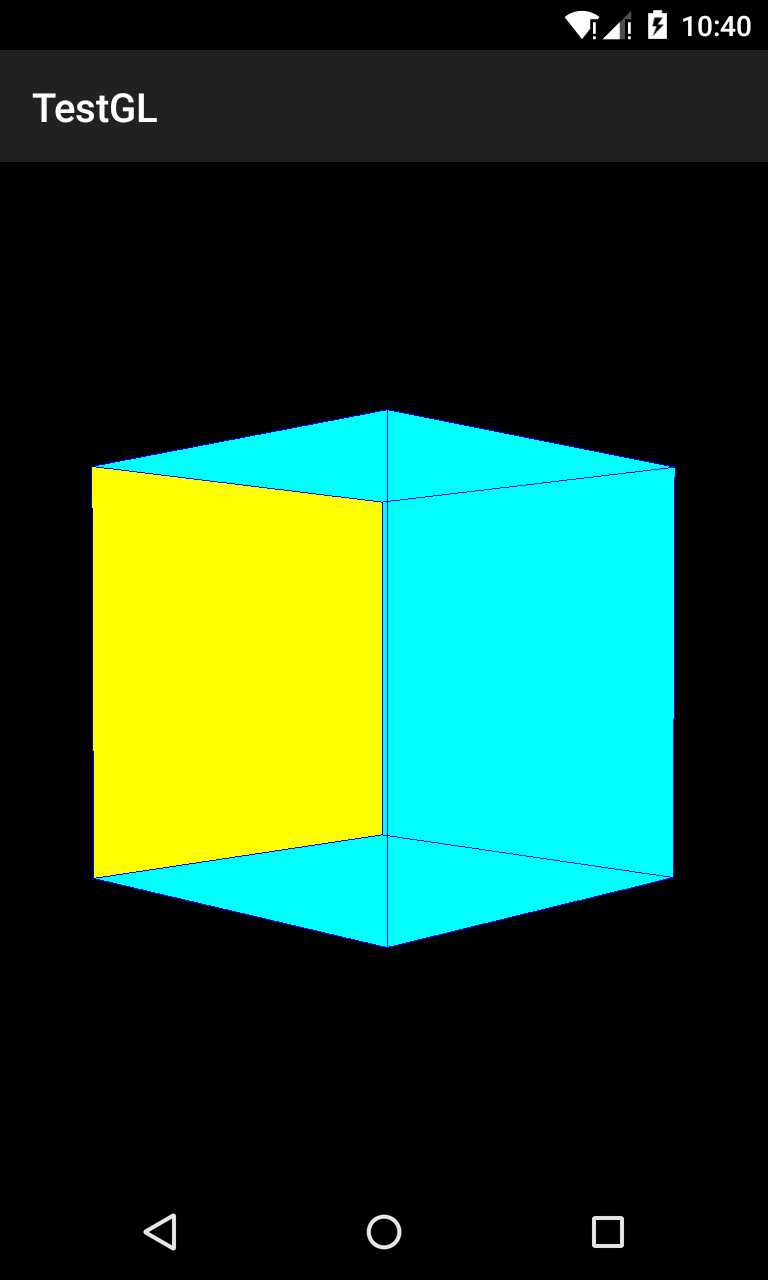
但是由于是前视，初始化的视图就不那么明显了：

造成这样是由于我定义的顶点数据的顺序造成的，在后面的直线（就是边缘线）被一起绘制的时候自然不会管我定义的立方体某个面的边缘有没有被覆盖，所以视觉上就出现了这个问题，我下一步会尝试解决这个遮挡问题。

以上。

opengl ES中的透视

标签：

原文地址：http://www.cnblogs.com/lhyz/p/4334704.html