标签:
在一次足球比赛罚点球时,罚球队员可以选择L,M,R三种不同射门路径;门将可以选择扑向左路或者右路(原则上讲他也可以守在右路)。
| l | r | |
| L | 4,-4 | 9,-9 |
| M | 6,-6 | 6,-6 |
| R | 9,-9 | 4,-4 |
该表表示各自的收益,其中,Lr对应的9表示当射手射向左路而门将扑向右路时,射手有90%的概率进球,-9表示门将有90%的概率丢球(10%概率射偏)。其他收益以此类推。 我们假设门将扑向右路的概率是Pr,那么门将扑向左路的概率是Pl=1-Pr。 那么,射手 选择左路的预期收益为 EU1(L,Pr) = Pl*U1(L,l) + Pr*U1(L,l) = (1-Pr)*4 + Pr*9 = 4 + 5*Pr; 选择中路的预期收益为 EU1(M,Pr) = Pl*U1(L,l) + Pr*U1(L,l) = (1-Pr)*6 + Pr*6 = 6; 选择右路的预期收益为 EU1(R,Pr) = Pl*U1(L,l) + Pr*U1(L,l) = (1-Pr)*9 + Pr*4 = 9 - 5*Pr;
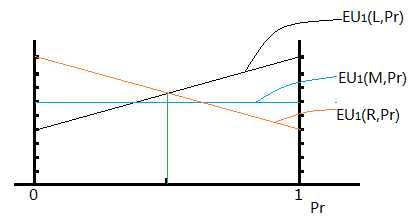
结论:从中路射门都不是一个最佳策略;不要选择在任何信念下都不是最佳策略的策略。
定义:参与者i的对策si是对手的策略s-i的最佳对策,当且仅当对于参与者i的所有其他策略si‘,U1(si,s-i)>=U1(si‘,s-i)
两个参与者都是公司的股东,他们都持有公司的股份并且平分利润。
si表示第i个股东为公司付出的精力。i=1,2。
总收益为4*(s1 + s2 + B*s1*s2)
所以对于每个参与者,他们能够获得的收益是1/2*4*(s1 + s2 + B*s1*s2) = 2*(s1 + s2 + B*s1*s2)
我们现在来考虑参与者1,他的付出是s1^2,s所以他的净收益为:2*(s1 + s2 + B*s1*s2) - s1^2
为了让收益最大,对s1求导得出收益导数为0的方程:s1 = 1 + B*s2
同理,对于s2,s2 = 1 + B*s1
我们这里设B=1/4。S=[1,4]。
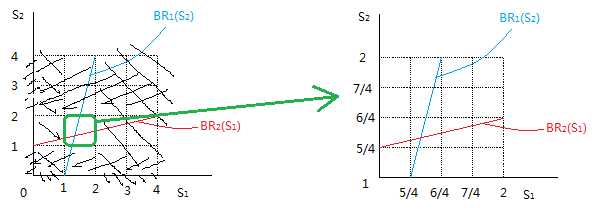
这里看一看到,因为s1的范围只在1和2之间,所以[0,1]和[3,4]是s1的劣势策略; 同理,[0,1]和[3,4]是s2的劣势策略。 所以剔除之后剩下了s1∈[1,2],s2∈[1,2]这个区间,我们将其放大四倍,发现了和原来一样的图。 然后我们就可以接待进行剔除了。 最后得到的点就是方程组: s1 = 1 + B*s2
s2 = 1 + B*s1
的解。 得出: s1 = s2 = 1/(B-1) (1/(B-1), 1/(B-1))这个点称为纳什均衡 Nash Equilibrium
这意味着博弈双方彼此都不想偏离纳什均衡点。在纳什均衡点处,双方都采取彼此的最佳对策。
标签:
原文地址:http://www.cnblogs.com/junealan/p/4338855.html