标签:
定义:
二叉堆是一颗被完全填满的二叉树,底层是从左到右填入。即完全二叉树。一棵高为h的完全二叉树有2^h到2^(h+1)-1个节点。这个还是很好证明的。由于完全二叉树很有规律,所以我们用数组而不是指针来表示它。
 对于任意位置i上的元素,左儿子位置为2i,右儿子(2i+1),父亲为[i/2](向下取整)
对于任意位置i上的元素,左儿子位置为2i,右儿子(2i+1),父亲为[i/2](向下取整)
1 typedef struct HeapStruct *PriorityQueue; 2 #define Mindata -10000 3 struct HeapStruct{ 4 int *Element;//成员数组 5 int Capacity;//容量 6 int Size;//当前大小 7 }; 8 9 PriorityQueue Initial(int MaxElements){ 10 PriorityQueue H; 11 H = (PriorityQueue)malloc(sizeof(struct HeapStruct)); 12 H->Capacity = MaxElements; 13 H->Size = 0; 14 H->Element = (int*)malloc(sizeof(int)*(MaxElements + 1)); 15 H->Element[0] = Mindata; 16 return H; 17 }
这里这个Mindata还是很有讲究的,后面解释。
堆可以分成最小堆和最大堆。
最小堆:对于每个节点X,X的父亲中的关键字小于或等于X。也就是对任意一棵树(子树),根节点总是最小的。
插入:
eg:插入14 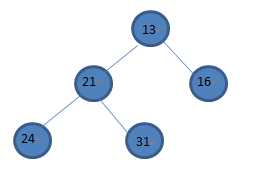
最初插入的位置是16的左节点,然后与16比,发现14比16小,那就违反了最小堆原则。那就把16放到14的位置,14上移动。
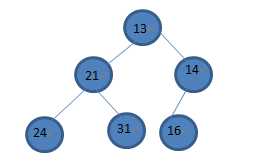
然后再和13比,发现已经比小了,那就符合最小堆条件,不需要再移动,所以插入完成。
1 void Insert(int X, PriorityQueue H){ 2 int i = 0; 3 if (H->Size == H->Capacity){ 4 printf("full!"); 5 } 6 else{ 7 for (i = ++H->Size; X < H->Element[i / 2]; i /= 2) 8 H->Element[i] = H->Element[i / 2]; 9 H->Element[i] = X; 10 } 11 }
这里就显示出MinData的好处了。 如果你现在要插入的是11,那么就比13这个原来的根节点还要小。但这时候根节点已经没有父节点的,而[1/2]=0, Element[0]又是你自己定义的最小的一个元素,所以11就直接留在根那块停下来了。当然不用Mindata做个判断语句当然也是可行的。
这里有用到一个策略叫做‘‘上滤",通俗一点就是把原来子节点要考虑的问题转移到他父节点去考虑。
DeleteMin:
其实和插入差不多。因为最小堆的最小值就是根,所以把根值取出即可。但我们不能取出之后就不管堆了啊,这时候可以把最后那个节点放到根上,然后再下滤来调整堆。比如像对于上面那个图,取出13后,把16放到13那个位置。但明显14比16小,所以需要下滤调整。
1 int DeleteMin(PriorityQueue H){ 2 3 int i,child; 4 if (H->Size == 0){ 5 printf("empty!"); 6 } 7 int LastNumber = H->Element[H->Size]; 8 int MinNumber = H->Element[1]; 9 H->Size--; 10 for (i = 1; 2 * i <= H->Size; i = child){ 11 child = 2 * i; 12 if (child != H->Size&&H->Element[child + 1] < H->Element[child]){ //这句很重要,因为可能只有一个孩子 13 child++; 14 } 15 if (LastNumber > H->Element[child]){ 16 H->Element[i] = H->Element[child]; 17 } 18 else 19 break; 20 } 21 H->Element[i] = LastNumber; 22 return MinNumber; 23 24 }
其他还有很多操作:
①DecreaseKey:上滤即可
②Delete: 先把key decrease成负无穷,然后再deleteMin即可。
③Min-Heapify:就是在假设左子树右子树都符合堆的性质时,根有可能不符合,进行调整使其符合。
代码和DeleteMin差不多:
1 void Min_Heapify(PriorityQueue H,int Num){ 2 int child, i; 3 int root = H->Element[Num]; 4 printf("%d", root); 5 for (i = Num; 2 * i <= H->Size; i = child){ 6 child = 2 * i; 7 if (child != H->Size&&H->Element[child + 1] < H->Element[child]){ //这句很重要,因为可能只有一个孩子 8 child++; 9 } 10 if (root > H->Element[child]){ 11 H->Element[i] = H->Element[child]; 12 } 13 else 14 break; 15 } 16 H->Element[i] =root; 17 }
④BuildHeap:
首先定理: 当用数组存储n个元素的堆时,叶节点下标分别为[n/2]+1,[n/2]+2……n.(向下取整)
因为①:Size为偶数时:2i=H->Size,所以i<=(H->Size)/2
②:Size为奇数时:2i+1=H->Size,所以i<=(H->Size-1)/2。
因此:我们建堆如下:只要从叶节点的前一个元素开始,依次对每一个元素进行一次维护最小堆性质的处理即可。再一次以上面的图为例。只要依次对14,21,13进行Min_Heapify就可以了。
1 void Build_Heap(PriorityQueue H, int* a,int length){ 2 H->Element = a; 3 H->Size = length; 4 int i; 5 for (i = length / 2 ; i >= 1; i--){ 6 Min_Heapify(H, i); 7 } 8 }
可以证明:Build_Heap的运行时间为O(N)。

标签:
原文地址:http://www.cnblogs.com/stezqy/p/4321379.html