标签:
数据分类的两个阶段:学习阶段(构造分类模型)和分类阶段(使用模型预测给定数据的类标号)和分类阶段(使用模型预测给定数据的类标号)。
构造一颗树,从根到叶子节点的路径,该叶子节点就存放着该元组的预测类。
决策树分类器的构造不需要任何领域知识和参数设置,因此适合于探测式知识发现。决策树可以处理高维数据。
分裂节点时,关于选择什么样的度量标准,主要分为三类:
1、ID3:信息增益;
2、C4.5:信息增益率;
3、基尼系数;
如何防止过拟合?
树剪枝;剪掉最不靠谱的分支;
方法:a)先剪枝;b)后剪枝;
尽管剪枝后的树一般比未剪枝的树更紧凑,但是他们仍然可能很大、很复杂。决策树可能受到重复和复制的困扰,使得他们很难解释。比如age<60,后面跟着age<45,出现了重复。复制是树中存在重复的子树。这些情况影响了决策树的准确率和可解释性。
两种解决办法:a)多元划分(基于组合属性的划分);b)使用不同形式的知识表示(如规则),而不是决策树。
IF-THEN规则——构造基于规则的分类器
可伸缩性与决策树归纳:
问题:已有的决策树算法,如ID3,C4.5,CART都是为相对较小的数据集设计的,限制训练元组。当需要把这些算法用于超大型现实世界的数据库的挖掘时,有效性就成了令人关注的问题。
一种方法就是:抽样;还是把训练数据放在内存中;
另一种方法就是:RainForest算法:AVC-集,描述该结点的训练元组。
自助乐观算法BOAT,扫描次数少较RainForest少,另一个优点是它可以增量地更新。
对于决策树,加入交互式方法,基于感知的分类(Perception-based Classification,PBC),基于多维可视化技术的交互式方法,允许用户在构建决策树时加上关于数据的背景。
基于贝叶斯定理:学过概率论的都知道这个定理,分清先验概率和后验概率。
可以参考之前的一篇利用贝叶斯做文本分类的文章:http://www.cnblogs.com/XBWer/p/3840736.html
当遇到多个属性值的时候,每个属性之间要满足相互独立的条件。
当遇到概率为0的情况时,可以采用拉普拉斯平滑,即加1(Stanford机器学习公开课上也提到过)。
使用IF-THEN规则:IF:规则前件或前提;THEN:规则的结论。
如果一个元组的数据对于规则X全部符合,那么我们说规则X被满足,并且覆盖了这个元组。
如何评估一条规则:覆盖率和准确率;覆盖率:覆盖的元组数/总元组数;准确率:正确分类的元组数/覆盖的元组数。
当一个元组可以触发多条规则,怎么办?
解决冲突的策略来决定激活哪一个规则,并对元组X指派它的类预测。
如何通过决策树提取IF-THEN规则,建立基于规则的分类器。与决策树(有时候可能会很大)相比,IF-THEN规则可能更加容易理解。
一个叶子节点对应一种规则显然是不科学的,因为数量太大,而且难于解释。
因此,如何修剪规则集is a problem
对于给定的规则前件,不能提高规则的估计准确率的额任何条件都可以剪掉(删除),从而泛化该规则。
对整个规则集的总体准确率没有贡献的任何规则也将剪去。
当然,在规则剪枝时也会有新的问题,因为这些规则不再是互斥和穷举的。
使用顺序覆盖算法的规则归纳:可以直接从训练数据提取IF-THEN规则(即不必产生决策树)。
常见的算法:AQ,CN2,RIPPER
一般策略:
可以看出,Learn_One_Rule的作用就是为当前累找出“最好的”规则。
那么,规则是如何生成的呢?
从一般到特殊。采用贪心的深度优先策略。每当面临添加一个新的属性测试到当前规则时,它根据训练样本选择最能提高规则质量属性的测试。
如何度量规则的质量呢?
1、熵(适合覆盖单个类的大量元组和少量其他类元组的条件)
2、信息增益(适合于具有高准确率并且覆盖许多正元组的规则)
3、覆盖率
规则剪枝:防止过拟合
P是正元组,N是负元组。eg,正元组:buy_computer=yes,负元组:buy_computer=no。
混淆矩阵:分类分类器识别不同类元组的一个有用工具。
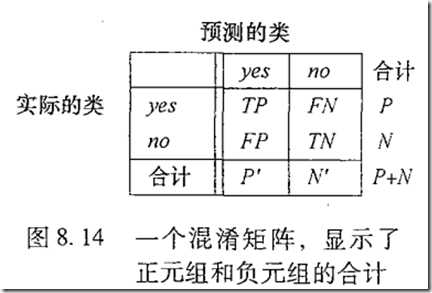
可以从矩阵中很容易看出准确率(识别率)。
灵敏性和特效性
精度和召回率
刚才这些度量是在假定所有的对象都是唯一可分类的前提下的。因此,当假定一个元组可以属于多个类的情况下,不要求返回类标号(即具体是属于哪一类的),而是要求返回类分布的概率。这时,准确率度量可以采用二次猜测试探:一个类预测被断定是正确的,如果它与最可能的或次可能的类一致。尽管这在某种程度上确实考虑了元组的非唯一分类,但它不是完全解。
:就是我们平时所做的,一部分作为训练集,一部分作为测试集。
这里可以参考Stanford机器学习课程第11课。
k折交叉验证
分层交叉验证
一般取k=10
最常用的是632自助法。
首先理解什么是显著性检验:
显著性检验(significance test)就是事先对总体(随机变量)的参数或总体分布形式做出一个假设,然后利用样本信息来判断这个假设(备则假设)是否合理,即判断总体的真实情况与原假设是否有显著性差异。或者说,显著性检验要判断样本与我们对总体所做的假设之间的差异是纯属机会变异,还是由我们所做的假设与总体真实情况之间不一致所引起的。 显著性检验是针对我们对总体所做的假设做检验,其原理就是“小概率事件实际不可能性原理”来接受或否定假设。
抽样实验会产生抽样误差,对实验资料进行比较分析时,不能仅凭两个结果(平均数或率)的不同就作出结论,而是要进行统计学分析,鉴别出两者差异是抽样误差引起的,还是由特定的实验处理引起的。
eg:
简而言之,基于多种分类方法建立多个不同的分类器,根据他们的预测结果,得出最终的分类结果。
装袋、提升和随机森林都是组合分类方法的例子
很简单,和自助法很像,又放回的抽样,创建k个模型,使用组合分类器,每个分类器都具有相同的权重,对新的元组进行分类,返回多数表决结果。
提升:每个分类器并不是具有相同的权重
AdaBoost:
转自:http://www.cnblogs.com/tornadomeet/archive/2012/11/06/2756361.html
每个分类器都是一棵决策树,那么组合分类器就是一个“森林”。
在机器学习中,随机森林由许多的决策树组成,因为这些决策树的形成采用了随机的方法,因此也叫做随机决策树。随机森林中的树之间是没有关联的。当测试数据进入随机森林时,其实就是让每一颗决策树进行分类,最后取所有决策树中分类结果最多的那类为最终的结果。因此随机森林是一个包含多个决策树的分类器,并且其输出的类别是由个别树输出的类别的众数而定。随机森林可以既可以处理属性为离散值的量,比如ID3算法,也可以处理属性为连续值的量,比如C4.5算法。另外,随机森林还可以用来进行无监督学习聚类和异常点检测。
随机森林由决策树组成,决策树实际上是将空间用超平面进行划分的一种方法,每次分割的时候,都将当前的空间一分为二,比如说下面的决策树(其属性的值都是连续的实数):
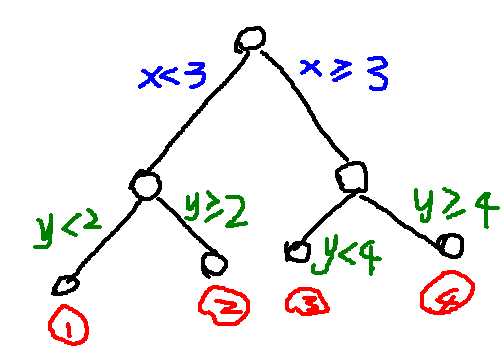
将空间划分为成的样子为:
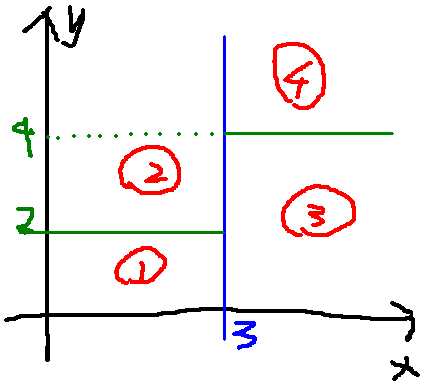
随机深林的优点:比较适合做多分类问题;训练和预测速度快;对训练数据的容错能力,是一种有效地估计缺失数据的一种方法,当数据集中有大比例的数据缺失时仍然可以保持精度不变;能够有效地处理大的数据集;可以处理没有删减的成千上万的变量;能够在分类的过程中可以生成一个泛化误差的内部无偏估计;能够检测到特征之间的相互影响以及重要性程度;不过出现过度拟合;实现简单容易并行化。
传统的分类算法旨在最小化分类误差。他们假定:假正例和假负例的代价是相等的。因此传统的分类算法不适合类不平衡数据。
其他方法:
1、过抽样(不涉及对分类模型结构的改变,改变训练集中的元组分布,使得稀有的类能够很好的代表,对正元组重复采样,使得结果训练集包含相同个数的正元组和负元组)
2、欠抽样(不涉及对分类模型结构的改变,改变训练集中的元组分布,减少负元组的数量)
3、阈值移动(不涉及对分类模型结构的改变,影响对新数据分类时模型如何决策)
4、组合技术
标签:
原文地址:http://www.cnblogs.com/XBWer/p/4340074.html