混沌图像---马丁迭代【密集恐惧症患者慎入】

标签：

      马丁迭代是我必需要讲的一个方程，因为之前看到一段由它生成图像的代码，我才开始研究混沌生成图像，并写了这个软件:YChaos生成混沌图像。马丁迭代图像的生成过程，如同生物的生长，一层层，一圈圈不停地变大变深变粗。虽然最终生成的图像看上去都差不多，但每一个参数下的图像的生成过程都不一样。最能体现混沌的是，马丁迭代的参数中，只要对任意一项，哪怕是极小的修改也会导致最终生成的数据完全不一样。

      似乎网上关于它的资料很少，我只找到这么几句：

     受Mandelbrot集产生思想的影响，Martin提出了一对公式，而利用该公式和同样简单的计算机程序便可产生非常新奇的图形，由于图形的产生过程会有爆炸现象出现，因此可以用来描述高层次的复杂及突变的现象，如天气的突然变冷、全球石油价格的暴涨以及股市行情的瞬息万变等。

其公式如下:

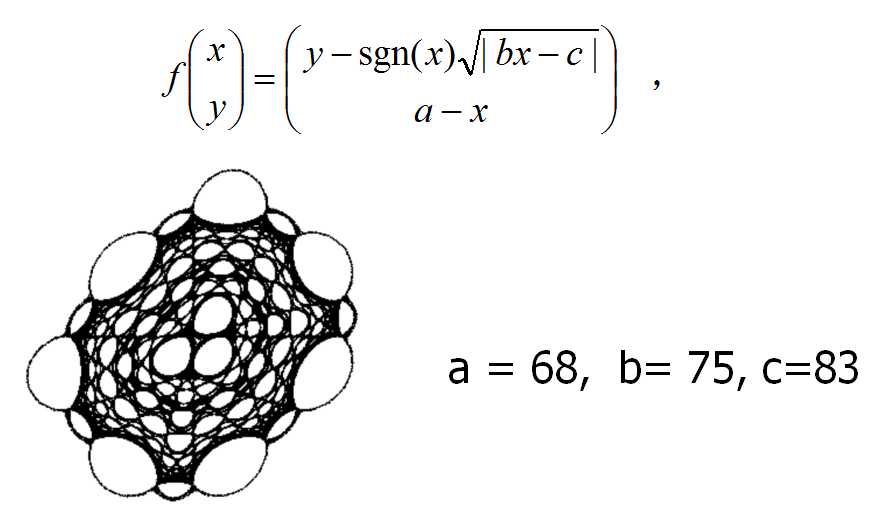
      这里使用我定义语法的脚本代码生成混沌图像。相关软件参见:YChaos生成混沌图像。如果你对数学生成图形图像感兴趣,欢迎加入QQ交流群: 367752815

脚本很简单:

[ScriptLines]
t=sqrt(abs(b*x - c))
m=if(x > EPSILON,y-t,y)
m=if(x < (-EPSILON),y+t,m)
y=a - x
x=m

[Variables]
a=0.680000
b=0.750000
c=0.830000
x=1.000000
y=1.000000

图像如下:

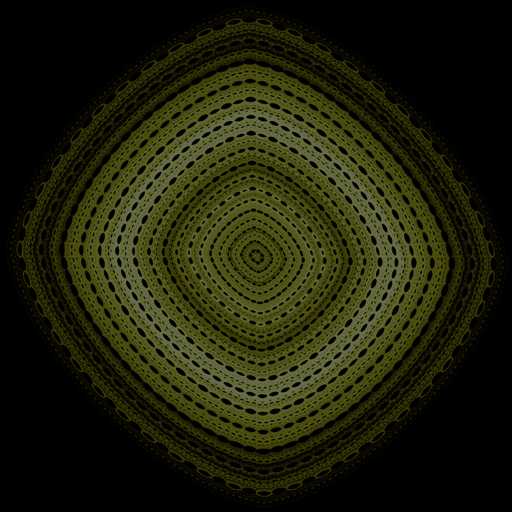
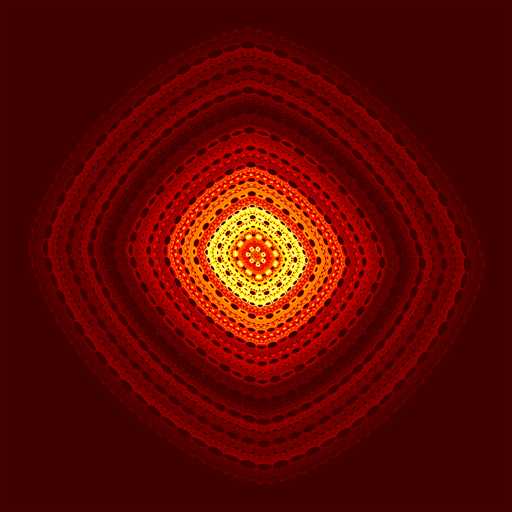
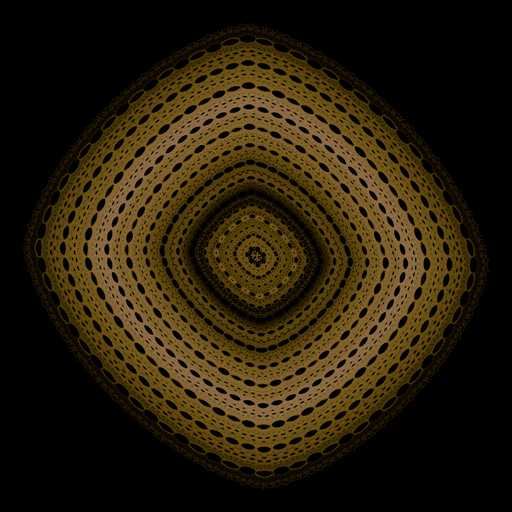
马丁迭代是一个膨胀的过程,与其他的混沌相比,它无法将其数值结果限定到一个有限的范围内,那我就试着对它限定一下:

[ScriptLines]
t=sqrt(abs(b*x - c))
m=if(x > EPSILON,y-t,y)
m=if(x < (-EPSILON),y+t,m)
y=s*(a - x)
x=m

[Variables]
a=0.680000
b=0.750000
c=0.830000
s=0.950000
x=1.000000
y=1.000000

相关软件:

YChaos生成混沌图像

相关文章:

混沌分形之马丁(Martin)迭代

混沌图像---马丁迭代【密集恐惧症患者慎入】

标签：

原文地址：http://www.cnblogs.com/WhyEngine/p/4330595.html