题目大意:
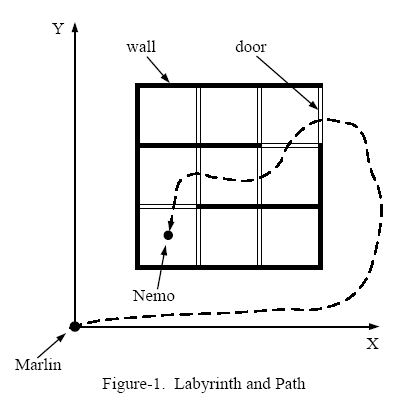
有一片方格区域,由一米的小方格构成,方格的边可能为墙意为不能通过,可能是空白,可能是门意为可以通过,一位名叫Nemo的孩子在方格的任意位置坐标,坐标为浮点类型。问一位名叫Marlin的人至少通过几个门才能找到Nemo。

解题思路:
做了好久,刚开始没思路不知道怎么建图,后来看了看discuss,可以根据左下角的点来建图,这时只需要记住两个方向即可,记住每个点左下角上方向为”1“,右方向为“0”。例如:map[I][J][0] =1 意思就是i,j点的右方向 是门可以通过 。map[i][j][1]=INF ,意思就是i,j点的上方向是墙。 编完感觉很对,但是discuss的数据过不了,原来,输入的数据建图之后会有空白的地方加入两个空白的格子连在一起既没有墙也没有门,这时只记为穿越一个门,但是一般队列可能会在别的路线先到达f1,f2.不先走连在一起空白格子。 这时穿越的门就不一定是最小的, 这时需要用到优先队列,一遍每次遍历先从穿越门最小的开始,最后找到的一定是最小的。
最后水了一把数据, 当f1,f2.在格子外面也需要考虑输出“0 ”。但是只是判断了f1,f2 是否在格子的上面或者右边就过了。
代码:

1 #include <algorithm> 2 #include <iostream> 3 #include <sstream> 4 #include <cstdlib> 5 #include <cstring> 6 #include <cstdio> 7 #include <string> 8 #include <bitset> 9 #include <vector> 10 #include <queue> 11 #include <stack> 12 #include <cmath> 13 #include <list> 14 //#include <map> 15 #include <set> 16 using namespace std; 17 /***************************************/ 18 #define ll long long 19 #define int64 __int64 20 /***************************************/ 21 const int INF = 0x7f7f7f7f; 22 const double eps = 1e-8; 23 const double PIE=acos(-1.0); 24 const int d1x[]= {0,-1,0,1}; 25 const int d1y[]= {-1,0,1,0}; 26 const int d2x[]= {0,-1,0,1}; 27 const int d2y[]= {1,0,-1,0}; 28 const int fx[]= {-1,-1,-1,0,0,1,1,1}; 29 const int fy[]= {-1,0,1,-1,1,-1,0,1}; 30 /***************************************/ 31 void openfile() 32 { 33 freopen("data.in","rb",stdin); 34 freopen("data.out","wb",stdout); 35 } 36 /**********************华丽丽的分割线,以上为模板部分*****************/ 37 int map[300][300][2]; //存储图 38 int vis[300][300],cnt[300][300]; //cnt计数 39 int maxx,maxy; 40 int sum; 41 struct node 42 { 43 int x,y; 44 bool operator < (const node &n1)const //优先队列从小到大排 45 { 46 return cnt[n1.x][n1.y]<cnt[x][y]; 47 } 48 }; 49 void BFS(int f1,int f2) 50 { 51 priority_queue<node >Q; 52 int i,j; 53 int x,y; 54 node ce; 55 for(i=0; i<=maxx; i++) 56 for(j=0; j<=maxy; j++) 57 cnt[i][j]=INF; //因为需要判断这个格子是否走过,用到最短路的这个点的cnt值加上map值是否小于i,j这个点的cnt值。 58 cnt[0][0]=0; 59 ce.x=0; 60 ce.y=0; 61 Q.push(ce); 62 while(!Q.empty()) 63 { 64 ce=Q.top(); 65 Q.pop(); 66 x=ce.x; 67 y=ce.y; 68 if (x==f1&&y==f2) 69 { 70 sum=cnt[x][y]; 71 return ; 72 } 73 if (y+1<=maxy&&cnt[x][y+1]>cnt[x][y]+map[x][y+1][0]) //向上走时是交于x,y+1的右方向的边 74 { 75 cnt[x][y+1]=cnt[x][y]+map[x][y+1][0]; 76 ce.x=x; 77 ce.y=y+1; 78 Q.push(ce); 79 } 80 if (y-1>=0&&cnt[x][y-1]>cnt[x][y]+map[x][y][0]) //向下走时是交于x,y的右方向的边 81 { 82 cnt[x][y-1]=cnt[x][y]+map[x][y][0]; 83 ce.x=x; 84 ce.y=y-1; 85 Q.push(ce); 86 } 87 if (x+1<=maxx&&cnt[x+1][y]>cnt[x][y]+map[x+1][y][1])//向右走时是交于x+1,y的上方向的边 88 { 89 cnt[x+1][y]=cnt[x][y]+map[x+1][y][1]; 90 ce.x=x+1; 91 ce.y=y; 92 Q.push(ce); 93 } 94 if (x-1>=0&&cnt[x-1][y]>cnt[x][y]+map[x][y][1])//向左走时是交于x,y的上方向的边 95 { 96 cnt[x-1][y]=cnt[x][y]+map[x][y][1]; 97 ce.x=x-1; 98 ce.y=y; 99 Q.push(ce); 100 } 101 } 102 sum=-1; 103 return ; 104 } 105 int main() 106 { 107 int m,n; 108 while(scanf("%d%d",&m,&n)!=EOF) 109 { 110 if (m==-1&&n==-1) 111 break; 112 sum=0; 113 int i,j; 114 int x,y,d,t; 115 memset(map,0,sizeof(map)); 116 memset(vis,0,sizeof(vis)); 117 memset(cnt,0,sizeof(cnt)); 118 maxx=-1; 119 maxy=-1; 120 for(i=0; i<m; i++) 121 { 122 scanf("%d%d%d%d",&x,&y,&d,&t); 123 for(j=0; j<t; j++) 124 { 125 if (d) //1 代表 向上的方向标记,0则相反。 126 { 127 map[x][y+j][d]=INF; //标记为墙 128 maxx=max(maxx,x); //找格子最大的x坐标 129 maxy=max(maxy,y+t);//找格子最大的y坐标 130 } 131 else 132 { 133 map[x+j][y][d]=INF; 134 maxx=max(maxx,x+t); 135 maxy=max(maxy,y); 136 } 137 } 138 } 139 int x1,y1,d1; 140 for(i=0; i<n; i++) 141 { 142 scanf("%d%d%d",&x1,&y1,&d1); 143 map[x1][y1][d1]=1; //标记为门 144 } 145 double f1,f2; 146 scanf("%lf%lf",&f1,&f2); 147 if(f1>maxx||f2>maxy) 148 { 149 printf("0\n"); 150 continue; 151 } 152 BFS(f1,f2); 153 printf("%d\n",sum); 154 } 155 return 0; 156 }
poj2049(Finding Nemo),布布扣,bubuko.com
原文地址:http://www.cnblogs.com/ZhaoPengkinghold/p/3765819.html