标签:
1、二次贝塞尔曲线
quadraticCurveTo(cpx,cpy,x,y) //cpx,cpy表示控制点的坐标,x,y表示终点坐标;
数学公式表示如下:
二次方贝兹曲线的路径由给定点P0、P1、P2的函数B(t)追踪:
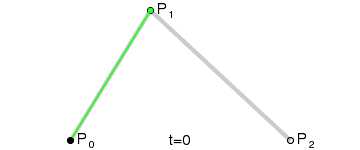
代码实例:
<!DOCTYPE html> <html> <head> <meta charset="utf-8"> <title>canvas直线</title> <meta name="Keywords" content=""> <meta name="author" content="@my_programmer"> <style type="text/css"> body, h1{margin:0;} canvas{margin: 20px;} </style> </head> <body onload="draw()"> <h1>二次贝塞尔曲线</h1> <canvas id="canvas" width=200 height=200 style="border: 1px solid #ccc;"></canvas> <script> function draw() { var canvas=document.getElementById(‘canvas‘); var context=canvas.getContext(‘2d‘); //绘制起始点、控制点、终点 context.beginPath(); context.moveTo(20,170); context.lineTo(130,40); context.lineTo(180,150); context.stroke(); //绘制2次贝塞尔曲线 context.beginPath(); context.moveTo(20,170); context.quadraticCurveTo(130,40,180,150); context.strokeStyle = "red"; context.stroke(); } </script> </body> </html>
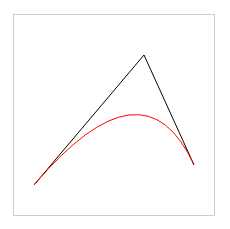
代码效果:
2、三次贝塞尔曲线
bezierCurveTo(cp1x,cp1y,cp2x,cp2y,x,y) //cp1x,cp1y表示第一个控制点的坐标,cp2x,cp2y表示第二个控制点的坐标,x,y表示终点的坐标;
数学公式表示如下:
P0、P1、P2、P3四个点在平面或在三维空间中定义了三次方贝兹曲线。曲线起始于P0走向P1,并从P2的方向来到P3。一般不会经过P1或P2;这两个点只是在那里提供方向资讯。P0和P1之间的间距,决定了曲线在转而趋进P3之前,走向P2方向的“长度有多长”。
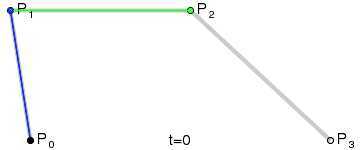
代码实例:
<!DOCTYPE html> <html> <head> <meta charset="utf-8"> <title>canvas直线</title> <meta name="Keywords" content=""> <meta name="Description" content=""> <style type="text/css"> body, h1{margin:0;} canvas{margin: 20px; } </style> </head> <body onload="draw()"> <h1>三次贝塞尔曲线</h1> <canvas id="canvas" width=200 height=200 style="border: 1px solid #ccc;"></canvas> <script> function draw() { var canvas=document.getElementById(‘canvas‘); var context=canvas.getContext(‘2d‘); //绘制起始点、控制点、终点 context.beginPath(); context.moveTo(25,175); context.lineTo(60,80); context.lineTo(150,30); context.lineTo(170,150); context.stroke(); //绘制3次贝塞尔曲线 context.beginPath(); context.moveTo(25,175); context.bezierCurveTo(60,80,150,30,170,150); context.strokeStyle = "red"; context.stroke(); } </script> </body> </html>
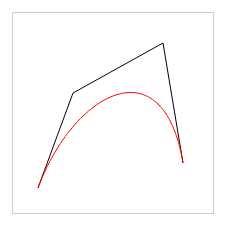
代码效果图:
标签:
原文地址:http://www.cnblogs.com/hf8051/p/4344469.html