标签:
A . 250

Problem Statement Some people are sitting in a row. Each person came here from some country. You have a theory that people from the same country are all sitting together. You decided to test this theory. You asked each person the same question: "How many people from your country (including you) are here?" You are given a vector <int> a containing their answers. The answers are given in the order in which the people sit in the row. (Note that some of the answers may be incorrect. See the examples for clarification.) If all the answers are consistent with your theory, return the number of different countries that are present. (Given that all answers are consistent with the theory, the number of countries can always be uniquely determined.) Otherwise, return -1. Definition Class: CountryGroup Method: solve Parameters: vector <int> Returns: int Method signature: int solve(vector <int> a) (be sure your method is public) Limits Time limit (s): 2.000 Memory limit (MB): 256 Stack limit (MB): 256 Constraints - The number of elements in a will be between 1 and 100, inclusive. - All elements of a will be between 1 and 100, inclusive. Examples 0) {2,2,3,3,3} Returns: 2 These answers are consistent with your theory. The first two people are from one country, the other three are from a different country. Thus, there are two countries and the correct return value is 2. 1) {1,1,1,1,1} Returns: 5 Here, each person comes from a different country. 2) {3,3} Returns: -1 These answers do not correspond to your theory. In particular, they are not even correct: there are only two people but each of them claims that there are three people from their country. 3) {4,4,4,4,1,1,2,2,3,3,3} Returns: 5 4) {2,1,2,2,1,2} Returns: -1 These answers do not correspond to your theory. It is possible that these are people from four different countries, but even if that were the case, we can tell that people from some countries are not sitting together. For example, consider the leftmost person. According to her answer, there are two people from her country. However, the person sitting next to her cannot be from the same country. This problem statement is the exclusive and proprietary property of TopCoder, Inc. Any unauthorized use or reproduction of this information without the prior written consent of TopCoder, Inc. is strictly prohibited. (c)2003, TopCoder, Inc. All rights reserved.
模拟 , 看看给出的串是否合法 。

#include <string> #include <vector> #include <algorithm> #include <cstring> using namespace std; const int N = 111; class CountryGroup { bool vis[N]; public: int solve( vector<int> x ) { memset( vis , 0 , sizeof vis ); int ans = 0 , n = (int) x.size() ; bool tag = true ; for( int i = 0 ; i < n ; ++i ) if( !vis[i] ) { if( i + x[i] > n ) { tag = false ; break ; } for( int j = i ; j < i + x[i] ; ++j ) { if( x[j] != x[i] ) { tag = false ; break ; } vis[j] = true ; } ans++ ; } if( !tag ) return -1 ; else return ans ; } };
B. 500

Problem Statement Alice and Bob are going to play a variant of the traditional rock-paper-scissors game. Their game is played using cards. Each card shows one of the three pictures: a rock, a paper, or scissors. There is a sufficient supply of cards of each type. Bob has already chosen a sequence of cards and he has arranged them into a row, face down. It is now Alice‘s turn to do the same. Once she does that, they will use the two sequences of cards to play the game: For each i, Alice‘s i-th card and Bob‘s i-th card will be revealed and compared using the standard rules of rock-paper-scissors. Whenever Alice‘s card wins, Alice gets a point. Alice gets no points for a loss or a tie. Alice has marked Bob‘s cards, so now she can tell which card has which symbol on it. You are given this information as a vector <int> card. Each element of card is between 0 and 2, inclusive: 0 is a rock, 1 is a paper, and 2 are scissors. You are also given an int score. Alice has just announced that she will get a total of score points. Let X be the number of sequences in which Alice can play her cards if she wants to achieve exactly score points. Return the value (X modulo 1,000,000,007). Definition Class: RockPaperScissorsMagicEasy Method: count Parameters: vector <int>, int Returns: int Method signature: int count(vector <int> card, int score) (be sure your method is public) Limits Time limit (s): 2.000 Memory limit (MB): 256 Stack limit (MB): 256 Constraints - The number of elements in card will be between 1 and 2,000, inclusive. - All elements of card will be between 0 and 2, inclusive. - score will be between 0 and 2,000, inclusive. Examples 0) {0,1,2} 2 Returns: 6 Bob has played his cards in the order rock-paper-scissors. Alice wants to score 2 points. Hence, she must win twice, and lose to Bob or tie him once. One possible way in which she can play her cards is paper-scissors-scissors: her paper beats Bob‘s rock (1 point), scissors beat paper (1 point), and scissors tie with scissors (0 points). There are five other ways how Alice can score 2 points: paper-scissors-paper, paper-paper-rock, paper-rock-rock, rock-scissors-rock, and scissors-scissors-rock. 1) {1,2} 0 Returns: 4 2) {2,2,1,0,0} 10 Returns: 0 3) {0,0,0,0,0,0,1,1,1,1,1,1,1,1,1,1,1,1,2,2,2,2,2,2,2,2,2,2,2,2,2,2,2} 7 Returns: 286226628 4) {0,1,2,0,1,2,2,1,0} 8 Returns: 18 This problem statement is the exclusive and proprietary property of TopCoder, Inc. Any unauthorized use or reproduction of this information without the prior written consent of TopCoder, Inc. is strictly prohibited. (c)2003, TopCoder, Inc. All rights reserved.
玩剪刀石头布, 每局赢了拿1分, 输了或者打平没分, 问能达到k 分的出拳发案数 。
设 dp[i][j] ...表示前i盘拿到 j 分的方案数

#include <string> #include <vector> #include <algorithm> #include <cstring> using namespace std; const int mod = 1e9+7; const int N = 2015; class RockPaperScissorsMagicEasy { long long dp[N][N]; public: int count( vector <int> card, int score) { int n = card.size(); memset( dp , 0 , sizeof dp ); dp[0][0] = 1 ; for( int i = 1 ; i <= n ; ++i ) { for( int j = 0 ; j <= i ; ++j ) { if( j > 0 ) dp[i][j] = ( dp[i][j] + dp[i-1][j-1] ) % mod ; dp[i][j] = ( dp[i][j] + 2 * dp[i-1][j] ) % mod ; } } int ans = (int) dp[n][score] ; return ans ; } };
C.1000

Problem Statement Alice and Bob are going to sing a song together. For simplicity, we will assign the numbers 1 through 1,000,000 to the pitches that occur in the song (from the lowest to the highest). Both Alice and Bob are able to sing all of these pitches. You are given a vector <int> pitch containing the pitches of all notes in the song, in order. Each note of the song will be sung by exactly one of our singers. Changing the pitch of one‘s voice is exhausting. Given a sequence of pitches to sing, the difficulty for the singer can be computed by summing up the differences between consecutive pitches. For example, the difficulty of the sequence 8, 8, 13, 12 is abs(8-8) + abs(13-8) + abs(12-13) = 0+5+1 = 6. The total difficulty of singing the song can be computed as the difficulty for Alice plus the difficulty for Bob. Return the smallest possible total difficulty of singing the given song. Definition Class: SingingEasy Method: solve Parameters: vector <int> Returns: int Method signature: int solve(vector <int> pitch) (be sure your method is public) Limits Time limit (s): 2.000 Memory limit (MB): 256 Stack limit (MB): 256 Constraints - The number of elements in pitches will be between 1 and 2,000, inclusive. - all elements in pitch will be between 1 and 1,000,000, inclusive. Examples 0) {1,3,8,12,13} Returns: 7 One optimal solution is to let Alice sing the first two notes and Bob the remaining three. Then, Alice will sing the sequence of pitches {1,3} and Bob will sing {8,12,13}. The difficulty for Alice is abs(3-1) = 2. The difficulty for Bob is abs(12-8) + abs(13-12) = 5. Thus, the total difficulty is 2+5 = 7. 1) {1,5,6,2,1} Returns: 3 One optimal solution is to let our singers sing in the order Alice-Bob-Bob-Alice-Alice. In this case Alice sings the sequence of pitches {1,2,1} and Bob sings {5,6}. Hence the difficulty for Alice is 2 and the difficulty for Bob is 1. 2) {5,5,5,5,4,4,4,4} Returns: 0 3) {1000000} Returns: 0 4) {24,13,2,4,54,23,12,53,12,23,42,13,53,12,24,12,11,24,42,52,12,32,42} Returns: 188 This problem statement is the exclusive and proprietary property of TopCoder, Inc. Any unauthorized use or reproduction of this information without the prior written consent of TopCoder, Inc. is strictly prohibited. (c)2003, TopCoder, Inc. All rights reserved.
两个人唱歌,换音要费用为音调差。
设dp[i][j] .. 表示唱到1个人第i个音, 另一个人唱到第j个音的最小费用。
转移的时候要注意某个人还未唱的情况。 用状态[0]表示

#include <string> #include <vector> #include <algorithm> #include <cstring> #include <cstdio> #include <iostream> #include <cmath> using namespace std; typedef long long LL; const int mod = 1e9+7; const LL inf = 1e17; const int N = 2015; class SingingEasy { long long dp[N][N] , x[N] ; public: int solve(vector <int> pitch) { int n = pitch.size(); for( int i = 0 ; i < n ; ++i ) x[i+1] = pitch[i] ; for( int i = 0 ; i <= n ; ++i ) { for( int j = 0 ; j <= n ; ++j ) { dp[i][j] = inf ; } } dp[1][0] = 0 ; for( int i = 1 ; i < n ; ++i ) { for( int j = 0 ; j < i ; ++j ) { if( !j ) { dp[i+1][0] = min( dp[i+1][0] , dp[i][0] + abs( x[i+1] -x[i] ) ); dp[i+1][i] = min( dp[i+1][i] , dp[i][0] ); } else { dp[i+1][i] = min( dp[i+1][i] , dp[i][j] + abs( x[i+1] - x[j] ) ); dp[i+1][j] = min( dp[i+1][j] , dp[i][j] + abs( x[i+1] - x[i] ) ); } } } LL ans = inf ; for( int i = 0 ; i < n ; ++i ) ans = min( ans , dp[n][i] ); return (int)ans; } };
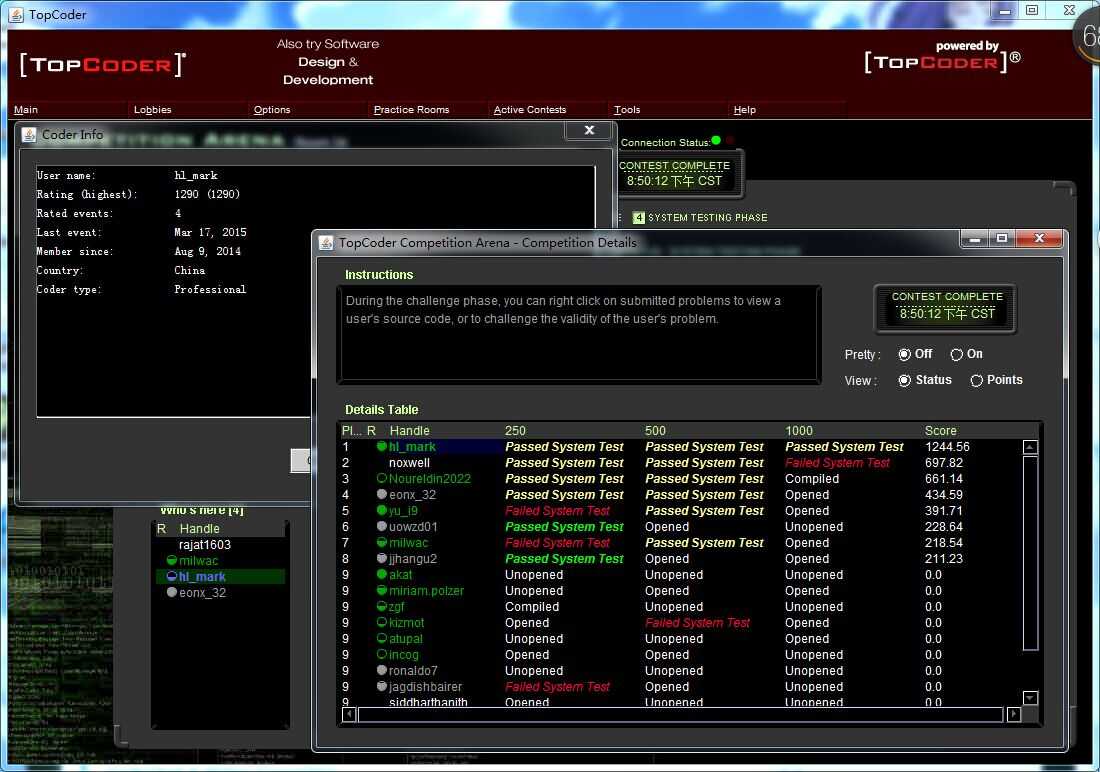
BC 拿ROOM rank1 之后 , 刚刚接触TC , 第一场DIV2 ROOM rank1 。
纪念一下。
标签:
原文地址:http://www.cnblogs.com/hlmark/p/4345553.html