URAL 1825. Ifrit Bomber 2 两圆的面积并

标签：几何   两圆面积并   

1825. Ifrit Bomber 2

The very first use of ifrit bottles caused mass protests from the world community. The UNESCO declared that ifrit bombardments were destroying the historical centers of large cities, which had a tremendous cultural importance.

Pitirim Schwartz corrected the behavior of ifrits so that the centers of the cities remained untouched. The destruction zone now was a ring instead of a disk: ifrits destroyed everything that was no closer than r and no farther than R from the impact point of the bottle.

To estimate the efficiency of carpet ifrit bombardments, Pitirim needs to be able to calculate the total area of the destruction zone in the case of dropping two ifrit bottles.

Input

The only input line contains integers d, r1, R1, r2, and R2, which are the distance between the impact points of the bottles, the inner and outer radii of destruction of the first bottle, and the inner and outer radii of destruction of the second bottle, respectively (0 ≤ d ≤ 15000; 1 ≤ ri <Ri ≤ 15000).

Output

Output the total destruction area with an absolute or relative error of at most 10?6.

Sample

input	output
200 100 300 200 300	353992.933435

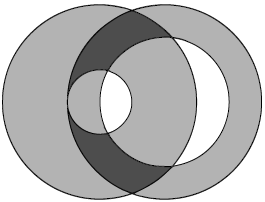
题意：给两个环，求这两个环覆盖的总面积。

给的数据是，两圆环距离d，第一个环的内圆半径r1，外圆半径R1，以及r2，R2。

做法：先把两个环各自的面积求出来，要算总覆盖面积的话，那接下来只用再计算出两者相交的面积即可。

两者相交的面积为=R1UR2 -R1Ur2 -r1UR2+r1Ur2.

其中R1UR2就是两个大圆 的面积并。

#include <stdio.h>
#include <stdlib.h>
#include <string.h> 
#include <string>
#include <iostream>
#include <algorithm>
using namespace std; 
#include <vector> 

const double eps = 1e-8;
const double PI = acos(-1.0);
int sgn(double x)
{
	if(fabs(x) < eps)return 0;
	if(x < 0)return -1;
	else return 1;
}

struct Point
{
	double x,y;
	Point(){}
	Point(double _x,double _y)
	{
		x = _x;y = _y;
	}
	Point operator -(const Point &b)const
	{
		return Point(x - b.x,y - b.y);
	}
	//叉积
	double operator ^(const Point &b)const
	{
		return x*b.y - y*b.x;
	}
	//点积
	double operator *(const Point &b)const
	{
		return x*b.x + y*b.y;
	}
	//绕原点旋转角度B（弧度值），后x,y的变化
	void transXY(double B)
	{
		double tx = x,ty = y;
		x = tx*cos(B) - ty*sin(B);
		y = tx*sin(B) + ty*cos(B);
	}
};

double dist(Point a,Point b)
{
	return sqrt((a-b)*(a-b));
}

double Area(Point c1,double r1,Point c2,double r2)
{
	double d = dist(c1,c2);
	if(r1 + r2 < d + eps)return 0;
	if(d < fabs(r1 - r2) + eps)
	{
		double r = min(r1,r2);
		return PI*r*r;
	}
	double x = (d*d + r1*r1 - r2*r2)/(2*d);
	double t1 = acos(x / r1);
	double t2 = acos((d - x)/r2);
	return r1*r1*t1 + r2*r2*t2 - d*r1*sin(t1);
}

int main()
{
	Point cir1,cir2;
	cir1.y=cir2.y=0;
	double d; 


	double r1,R1,r2,R2;
	while(cin>>d>>r1>>R1>>r2>>R2)
	{
		cir1.x=0;
		cir2.x=d;
 
		printf("%lf\n",PI*R1*R1-PI*r1*r1+PI*R2*R2-PI*r2*r2-(Area(cir1,R1,cir2,R2)-Area(cir1,R1,cir2,r2)-Area(cir1,r1,cir2,R2)+Area(cir1,r1,cir2,r2)));
	}
	return 0;
}

URAL 1825. Ifrit Bomber 2 两圆的面积并

标签：几何   两圆面积并   

原文地址：http://blog.csdn.net/u013532224/article/details/44348721