标签:
背景
在开发路径插件时,需要解决以下问题:获得路径上某一点到路径起点的曲线长度;给定曲线长度,返回路径上点的位置。路径是由三次样条(Spline)组成的,三次样条就是最高次数为 3 的一元多项式。设样条为 P(t) = f(t), 只要知道 t 就可以得到具体位置的坐标、一阶导等信息。设样条曲线长度为 s,那么要求的就是 t-s 和 s-t 的关系。不幸的是,曲线长度的计算没有解析解,只有数值方法。数值方法不适用于游戏中的时时运算,对性能影响太大。但是,如果事先对 s-t 或 t-s 曲线采样,然后运行时找到最接近的采样数据,就可以计算出大概的结果了。这种办法有两个问题需要解决:如何采样;基于采样数据如何根据 t 计算 s 或根据 s 计算 t。
分析
多段样条组成的路径长度不同、参数不同,需要他们的采样和计算结果具有相同的误差范围,这样才能保证一个匀速运动的物体经过不同样条时看起来没有变速,所以必须引入一个误差的概念。采样时误差越小、路径越长,采样的数据量越大。关于计算,最开始想到的是最小二乘法进行曲线拟合。但后来发现,最小二乘法只能保证已知采样点处误差最小,而无法保证采样点之间的准确程度,甚至会出现不单调的情况。然后想到的是使用 Catmull-Rom 样条来平滑穿过这些点,但是同样不能保证单调,而且端点问题很难处理。
采样
最开始使用指定采样数量、等距离采样的方法。这种方法的缺点就是,无法控制误差。要考虑误差,就得关心曲线的变化过程。
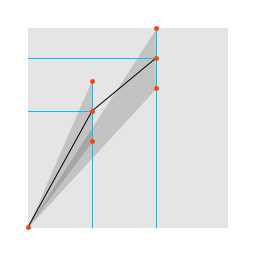
以极小的 dt 来计算 s,同时判断当前 s 是否应该存储到采样表。如图,在相邻两个点之间,认为曲线是直线,那么在给定误差范围内,直线的斜率也是一个范围;然后计算下一个点处的 s,考虑直线斜率的范围,如果这个范围与之前的范围有交集,那么交集作为新的斜率范围;如果没有交集,那么前一点处应当添加新采样数据,采样值取斜率范围内的中点,然后重新计算新的斜率范围。
Vector3 lastPoint = _c0, currentPoint; Vector2 currentSample = Vector2.zero, baseSample = Vector2.zero, newSample; float currentMaxSlope, maxSlope = float.MaxValue; float currentMinSlope, minSlope = float.MinValue; // 估算长度、分段数 for (int i = 1; i <= minSegments; i++) { currentPoint = GetPoint(i / (float)minSegments); currentSample.y += (currentPoint - lastPoint).magnitude; lastPoint = currentPoint; } int segments = Mathf.Clamp((int)(currentSample.y * segmentsFactor / _error) + 1, minSegments, maxSegments); List<Vector2> samples = new List<Vector2>((int)(segments * 0.1f) + 1); samples.Add(baseSample); lastPoint = _c0; currentSample = Vector2.zero; for (int i = 1; i <= segments; i++) { // 计算长度 currentPoint = GetPoint(currentSample.x = i / (float)segments); currentSample.y += (currentPoint - lastPoint).magnitude; lastPoint = currentPoint; // 计算斜率范围 currentMaxSlope = (currentSample.y + _error - baseSample.y) / (currentSample.x - baseSample.x); currentMinSlope = (currentSample.y - _error - baseSample.y) / (currentSample.x - baseSample.x); // 斜率范围无交集,需要添加记录采样 if (currentMaxSlope < minSlope || currentMinSlope > maxSlope) { // 添加上一个位置,取斜率范围平均值 newSample.x = (i - 1) / (float)segments; newSample.y = (newSample.x - baseSample.x) * (minSlope + maxSlope) * 0.5f + baseSample.y; samples.Add(baseSample = newSample); // 重置斜率范围 maxSlope = (currentSample.y + _error - baseSample.y) / (currentSample.x - baseSample.x); minSlope = (currentSample.y - _error - baseSample.y) / (currentSample.x - baseSample.x); } else { // 计算斜率范围交集 if (currentMaxSlope < maxSlope) maxSlope = currentMaxSlope; if (currentMinSlope > minSlope) minSlope = currentMinSlope; } } // 添加最后一个采样点 samples.Add(currentSample);
计算
采样过程已经保证了误差在指定值以下,所以计算时直接在两个采样值之间线性插值即可。那么如何找到最接近的采样数据呢?这里使用的方法不是折半查找,而是先估计然后线性查找(如果需要更快的话,可以考虑把折半查找的“折半”换成“估计”)。
/// <summary> /// 根据参数 t 获取长度 /// </summary> public float GetLength(float t) { if (Utility.IsNullOrEmpty(_samples)) CalculateLength(); if (t >= 1f) return _samples[_samples.Length - 1].y; if (t <= 0f) return 0f; int index = (int)(t * _samples.Length); Vector2 baseSample; if (_samples[index].x > t) { while (_samples[--index].x > t) ; baseSample = _samples[index++]; } else { while (_samples[++index].x < t) ; baseSample = _samples[index - 1]; } return baseSample.y + (t - baseSample.x) * (_samples[index].y - baseSample.y) / (_samples[index].x - baseSample.x); } /// <summary> /// 通过长度获取位置(返回值为参数 t) /// </summary> public float GetTimeAtLength(float s) { if (Utility.IsNullOrEmpty(_samples)) CalculateLength(); if (s >= _samples[_samples.Length - 1].y) return 1f; if (s <= 0f) return 0f; int index = (int)(s / _samples[_samples.Length - 1].y * _samples.Length); Vector2 baseSample; if (_samples[index].y > s) { while (_samples[--index].y > s) ; baseSample = _samples[index++]; } else { while (_samples[++index].y < s) ; baseSample = _samples[index - 1]; } return baseSample.x + (s - baseSample.y) * (_samples[index].x - baseSample.x) / (_samples[index].y - baseSample.y); }
结果
通过验证,这种方法的效果非常好,采样点数量很少,精确度却很高。并且精确度提高一个数量级时,采样数量通常只增加一到两倍。移动物体时表现的非常平滑,在多段样条间移动无论样条差异多大都很平稳。
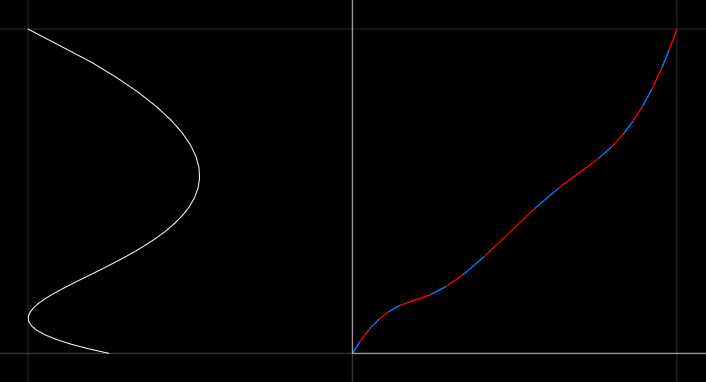
【下图:样条长度17.2,精确度0.01,采样数量20】
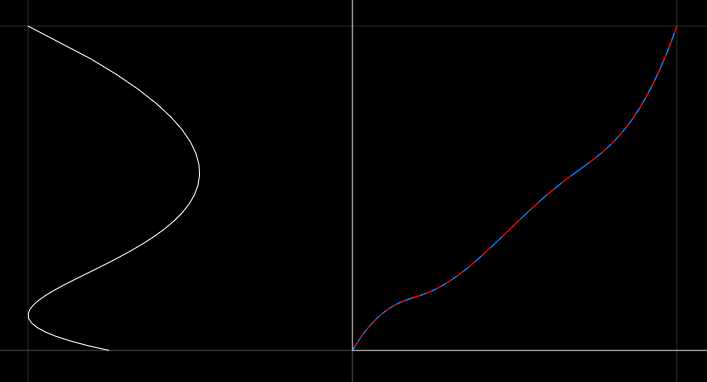
【下图:样条长度17.2,精确度0.001,采样数量64】
打个小广告:Unity 插件 White Cat‘s Path & Tween 已经提交审核,做插件花了很多时间,工作都没找,希望大家买买买 :-)
插件功能强大、操作简单,不需要编程即可使用,当然也支持编程交互。含有很多例子,包括路径和插值动画。详情页面:等审核完成后更新。
标签:
原文地址:http://www.cnblogs.com/whitecat/p/4346138.html