标签:
绘制曲线有几种思路:
1、通过quadraticCurveTo(controlX, controlY, endX, endY)方法来绘制二次曲线
2、通过bezierCurveTo(controlX1, controlY1, controlX2, controlY2, endX, endY)方法,来绘制贝塞尔曲线
3、通过画圆的方法arc(x, y, radius, startAngle, endAngle, antiClockwise)来取得某一段圆弧,作为要画出的曲线
1、二次曲线quadraticCurveTo
quadraticCurveTo(cpx,cpy,x,y)
二次曲线也称二次贝塞尔曲线或圆锥曲线或圆锥截线,是直圆锥面的两腔被一平面所截而得的曲线。当截面不通过锥面的顶点时,曲线可能是圆、椭圆、双曲线、抛物线。当截面通过锥面 的顶点时,曲线退缩成一点、一直线或二相交直线。在截面上的直角坐标系(x,y)之下,这些曲线的方程是x,y的二元二次方程
数学公式表示如下:
二次方贝兹曲线的路径由给定点P0、P1、P2的函数B(t)追踪:
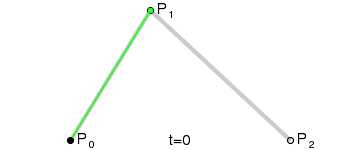
代码实例:
<!DOCTYPE html>
<html>
<head>
<meta
charset="utf-8">
<title>canvas直线</title>
<meta
name="Keywords" content="">
<meta name="author"
content="@my_programmer">
<style type="text/css">
body,
h1{margin:0;}
canvas{margin:
20px;}
</style>
</head>
<body
onload="draw()">
<h1>二次贝塞尔曲线</h1>
<canvas id="canvas"
width=200 height=200 style="border: 1px solid
#ccc;"></canvas>
<script>
function draw() {
var
canvas=document.getElementById(‘canvas‘);
var
context=canvas.getContext(‘2d‘);
//绘制起始点、控制点、终点
context.beginPath();
context.moveTo(20,170);
context.lineTo(130,40);
context.lineTo(180,150);
context.stroke();
//绘制2次贝塞尔曲线
context.beginPath();
context.moveTo(20,170);
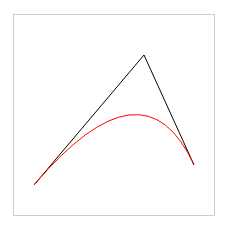
context.quadraticCurveTo(130,40,180,150);
context.strokeStyle = "red";
context.stroke();
}
</script>
</body>
</html>
代码效果:
2、贝塞尔曲线
bezierCurveTo(cp1x,cp1y,cp2x,cp2y,x,y)
贝塞尔曲线(Bézier curve),又称贝兹曲线或贝济埃曲线,是应用于二维图形应用程序的数学曲线。一般的矢量图形软件通过它来精确画出曲线,贝兹曲线由线段与节点组成,节点是可拖动的支点,线段像可伸缩的皮筋,我们在绘图工具上看到的钢笔工具就是来做这种矢量曲线的。当然在一些比较成熟的位图软件中也有贝塞尔曲线工具,如PhotoShop等。在Flash4中还没有完整的曲线工具,而在Flash5里面已经提供出贝塞尔曲线工具。
和二次曲线类似,它的函数是:bezierCurveTo()。贝塞尔曲线和二次曲线不同的是,它有2个控制点。二次曲线是有一个无形的控制点在拉动曲线,而贝塞尔曲线就是2个控制点在拉动曲线。
数学公式表示如下:
P0、P1、P2、P3四个点在平面或在三维空间中定义了三次方贝兹曲线。曲线起始于P0走向P1,并从P2的方向来到P3。一般不会经过P1或P2;这两个点只是在那里提供方向资讯。P0和P1之间的间距,决定了曲线在转而趋进P3之前,走向P2方向的“长度有多长”。
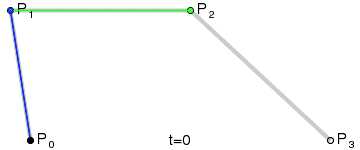
代码实例:
<!DOCTYPE html>
<html>
<head>
<meta charset="utf-8">
<title>canvas直线</title>
<meta name="Keywords" content="">
<meta name="Description" content="">
<style type="text/css">
body, h1{margin:0;}
canvas{margin: 20px; }
</style>
</head>
<body onload="draw()">
<h1>三次贝塞尔曲线</h1>
<canvas id="canvas" width=200 height=200 style="border: 1px solid #ccc;"></canvas>
<script>
function draw() {
var canvas=document.getElementById(‘canvas‘);
var context=canvas.getContext(‘2d‘);
//绘制起始点、控制点、终点
context.beginPath();
context.moveTo(25,175);
context.lineTo(60,80);
context.lineTo(150,30);
context.lineTo(170,150);
context.stroke();
//绘制3次贝塞尔曲线
context.beginPath();
context.moveTo(25,175);
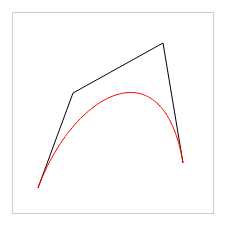
context.bezierCurveTo(60,80,150,30,170,150);
context.strokeStyle = "red";
context.stroke();
}
</script>
</body>
</html>
代码效果图:
3、圆弧线
arc(x, y, radius, startAngle, endAngle, antiClockwise)
所谓弧度就是一个圆周的一部分,可以用圆心(参数1、2)和圆的扇形半径(参数3)来表示。为了表示弧度的范围,必须定义弧度的起点(参数4)和终点(参数5),以及它的方向(参数6)。
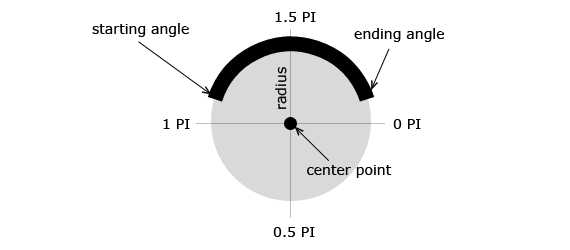
示例一个简单的弧度:
<!DOCTYPE HTML> <html> <head> <style> #myCanvas { border: 1px solid #9C9898; } </style> </head> <body> <canvas id="myCanvas" width="600" height="300"></canvas> <script> function PI(deg) { return deg/180*Math.PI; } var canvas = document.getElementById(‘myCanvas‘); var context = canvas.getContext(‘2d‘); var pi=Math.PI; context.beginPath(); context.arc(200, 200, 100, PI(-90), PI(0), false); context.lineWidth = 10; context.strokeStyle = ‘black‘; context.stroke(); </script> </body> </html>
标签:
原文地址:http://www.cnblogs.com/hf8051/p/4346364.html