跳台阶问题（变态跳台阶）的三种解法

标签：

题目1：一个台阶总共有n级，如果一次可以跳1级，也可以跳2级。求总共有多少总跳法，并分析算法的时间复杂度。

们把n级台阶时的跳法看成是n的函数，记为f(n)。当n>2时，第一次跳的时候就有两种不同的选择：一是第一次只跳1级，此时跳法数目等于后面剩下的n-1级台阶的跳法数目，即为f(n-1)；另外一种选择是第一次跳2级，此时跳法数目等于后面剩下的n-2级台阶的跳法数目，即为f(n-2)。因此n级台阶时的不同跳法的总数f(n)=f(n-1)+(f-2)。

我们把上面的分析用一个公式总结如下：

          /  1                               n=1
f(n)=      2                              n=2
          \  f(n-1)+(f-2)               n>2

分析到这里，相信很多人都能看出这就是我们熟悉的Fibonacci序列。

#include<stdio.h>
#include<string.h>
//递归解法
int solution1(int n)
{
    if(n == 0 || n == 1) return 1;
    else return solution1(n-1) + solution1(n-2);
}
//非递归解法
int solution2(int n)
{
    int f[100];
    f[0] = 1;
    f[1] = 1;
    for(int i=2; i<=n; ++i)
       f[i] = f[i-1] + f[i-2];
    return f[n];
}
//滚动数组解法
int solution3(int n)
{
int F[3]={0,1,2};
if(n<=2)
{
   return F[n];
}
for(int i=3;i<=n;i++)
{
F[0]=F[1];
F[1]=F[2];
F[2]=F[0]+F[1];
}
return F[2];
}
int main()
{
int n;
printf("请输入台阶个数：");
scanf("%d",&n);
int sum1= solution1(n);
        int sum2= solution2(n);
        int sum3= solution3(n);
printf("sum1=%d,sum2=%d,sum3=%d\n",sum1,sum2,sum3);
return 0;
}

题目2：一个台阶总共有n级，如果一次可以跳1级，也可以跳2级......它也可以跳上n级。此时该青蛙跳上一个n级的台阶总共有多少种跳法？
   分析：用Fib(n)表示青蛙跳上n阶台阶的跳法数，青蛙一次性跳上n阶台阶的跳法数1(n阶跳)，设定Fib(0) = 1；
       当n = 1 时， 只有一种跳法，即1阶跳：Fib(1) = 1;
       当n = 2 时， 有两种跳的方式，一阶跳和二阶跳：Fib(2) = Fib(1) + Fib(0) = 2;
       当n = 3 时，有三种跳的方式，第一次跳出一阶后，后面还有Fib(3-1)中跳法； 第一次跳出二阶后，后面还有Fib(3-2)中跳法；第一次跳出三阶后，后面还有Fib(3-3)中跳法
        Fib(3) = Fib(2) + Fib(1)+Fib(0)=4;
       当n = n 时，共有n种跳的方式，第一次跳出一阶后，后面还有Fib(n-1)中跳法； 第一次跳出二阶后，后面还有Fib(n-2)中跳法..........................第一次跳出n阶后，后面还有 Fib(n-n)中跳法.
       Fib(n) = Fib(n-1)+Fib(n-2)+Fib(n-3)+..........+Fib(n-n)=Fib(0)+Fib(1)+Fib(2)+.......+Fib(n-1)
      又因为Fib(n-1)=Fib(0)+Fib(1)+Fib(2)+.......+Fib(n-2)
      两式相减得：Fib(n)-Fib(n-1)=Fib(n-1)         =====》  Fib(n) = 2*Fib(n-1)     n >= 2
      递归等式如下：

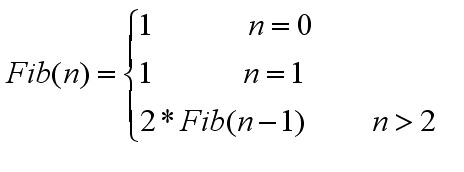
//变态跳
int solution4(int n)
{
    if(n == 0 || n == 1)
return 1;
    else
return 2*solution4(n-1);
}

//变态跳滚动数组
int solution5(int n)
{
int F[2]={0,1};
if(n < 2)
return F[n];

for(int i=2;i<=n;i++)
{
F[0]=F[1];
F[1]=2*F[0];
}
return F[1];
}

跳台阶问题（变态跳台阶）的三种解法

标签：

原文地址：http://blog.csdn.net/u014082714/article/details/44406917