hdu 3367 Pseudoforest（并查集）

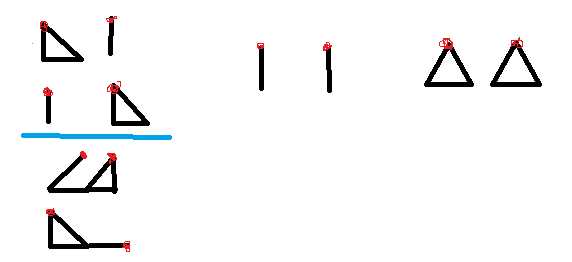
 1 #include<iostream>
 2 #include<cstdio>
 3 #include<cstdlib>
 4 #include<cstring>
 5 #include<string>
 6 #include<queue>
 7 #include<algorithm>
 8 #include<map>
 9 #include<iomanip>
10 #include<climits>
11 #include<string.h>
12 #include<cmath>
13 #include<stdlib.h>
14 #include<vector>
15 #include<stack>
16 #include<set>
17 #define INF 1e7
18 #define MAXN 10010
19 #define maxn 1000010
20 #define Mod 1000007
21 #define N 1010
22 using namespace std;
23 typedef long long LL;
24 
25 struct node{ 
26     int u, v, w; 
27     bool operator <(const node a) const{
28         return w > a.w;
29     }
30 }e[100010];
31 int fa[100010];
32 bool flag[100010];
33 int n, m;
34 
35 int findset(int x)
36 {
37     return fa[x] = fa[x] == x ? x : findset(fa[x]);
38 }
39 
40 int main()
41 {
42     int u, v;
43     while (~scanf("%d%d", &n, &m),n+m) {
44         for (int i = 0; i <= n; ++i) {
45             fa[i] = i, flag[i] = false;
46         }
47         for (int i = 0; i < m; ++i) {
48             cin >> e[i].u >> e[i].v >> e[i].w;
49         }
50         sort(e, e + m);
51         int ans = 0;
52         for (int i = 0; i < m; ++i) {
53             int x = findset(e[i].u);
54             int y = findset(e[i].v);
55             if (x != y) {
56                 if (!flag[x] && !flag[y]) {
57                     ans += e[i].w;
58                     fa[x] = y;
59                 }
60                 else if (!flag[x] && flag[y]) {
61                     ans += e[i].w;
62                     fa[x] = y;
63                     flag[y] = true;
64                 }
65                 else if (flag[x] && !flag[y]) {
66                     ans += e[i].w;
67                     fa[y] = x;
68                     flag[x] = true;
69                 }
70             }
71             else {
72                 if (!flag[x]) {
73                     flag[x] = true;
74                     ans += e[i].w;
75                 }
76                 else if (!flag[y])
77                 {
78                     flag[y] = true;
79                     ans += e[i].w;
80                 }
81             }
82         }
83         cout << ans << endl;
84     }
85     return 0;
86 }