Robust Mesh Watermarking

标签：

之前看了一篇题为"Robust Mesh Watermarking"的论文，查阅资料的时候发现了一篇与之很相似的名为"三维模型数字水印系统的设计与实现"的中文论文，在中文论文的帮助下，总算对网格水印有了一定的了解，简单整理了一下。

    由于知识版权保护的需要，数字水印技术应运而生。目前，图像、视频、音频、文本的水印研究已经比较成熟，但是三维模型水印的研究还相对匮乏。然而随着三维模型在网络上传播的日益增多，三维模型知识版权的保护也有了一定的研究意义。由于三维模型自身的特点，对嵌入其中的水印提出了不同于传统水印的要求：

• 健壮性
• 可工作在任意的网格上
• 保持原有的连接
• 不可感知

传统的水印一般分为时/空域水印和频域水印。在图像中，空域水印通过直接改变图像的像素来完成（比如早年提出的LSB算法），这类算法复杂度低，效率高，但缺乏健壮性，很容易被去除或破坏；

而频域（也称变换域）则是通过将图像转换到变换域，通过改变变换域中的某些参数来嵌入水印信息。这类变化主要包括DCT、DFT、DWT等。这类算法由于鲁棒性高，得到了普遍的研究。

对于网格而言，没有频域这一表示，因此需要寻找合适的表示方法来类比图像中的频域，本文的作者的出发点就是将图像中的频谱表示方式扩展到网格中来，他们的思路如下：

缺乏进行频率分解的某种自然的参数化方法（无DCT等）à网格多分辨率表示

没有自然的采样 à网格配准和重采样

以下就论文中提到的水印生成、嵌入及提取方法进行整理

水印生成：

以原模型文件MD5加密后的MD5值作为密钥, 将此密钥作为伪随机数生成器的种子, 从均值为0、方差为l 的高斯分布中取 M个随机实数作为水印w = {w₀,w_l, …… w_m-1 },

Key = MD5(models)；

W = Random (key)

W ~ N（0，1）

水印嵌入：

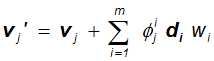
w：水印

Φ：基函数系数

d：水印嵌方向

矩阵形式为： V‘ = V + BW

矩阵X分量形式为：

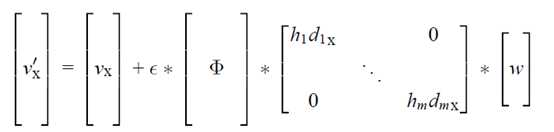
V_X‘ ：加入水印后网格顶点的X坐标

V_X ：原始网格顶点X坐标

ε：用户自定义的全局参数，用来控制水印嵌入的深度

Φ：是一个n x m的矩阵，由基函数组成的矩阵，其中矩阵中的项表示基函数Φⁱ 在顶点j处的标量系数

hd_x： 是一个 m x n 的对角矩阵，其中d_x是全局位移趋势d_i的X分量，h_i为第i个基函数的"幅度"

W ：水印

下面介绍、di、hi的生成，由于在生成这些值的过程中用到了PM算法，在这之前先简单介绍下渐进网格（Progressive Meshes， PM）算法

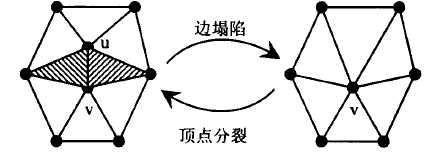
下图为边塌陷与顶点分裂对照图，在左图的网格中，顶点uv之间的边动过边塌陷后被去掉了，u点被合并到了v点，在边塌陷的过程中，记录原顶点和新顶点之间的位置以及顶点之间的连接关系的变动，从而可以通过右图的顶点v点分裂可以分裂出点u，然后恢复出uv之间的边。整个边塌陷去掉的是原始网格中能量较小的边，具体的能量函数此处不做讨论。

    在每次点分裂过程中，计算几何的幅度h：

• 首先，用当前点的1-领域的质心来表示（预测）当前点分裂后新产生的点，
• 然后，根据当前点的1-领域计算表面法向量
• 最后，h为表面法向量与实际分裂出的新点坐标与预测的新点左边之差之间的点乘，即h = 表面法向量.（实际新点坐标-预测新点坐标）

之后，从若干（作者没有交代具体次数）次点分裂操作中，选出前m次h最大的操作，在这m次操作对应的原始点上生成基函数。

对于每次塌陷，计算"边界"B_i：由塌陷点i的当前邻居经过追踪点分裂操作之后扩展的邻居集合。计算半径r_jⁱ ：对于每个顶点V_j，计算边界内的点C_i到它的距离，当Ci位于边界中心时，半径为0，C_i位于边界上或边界外时，半径为1，其他情况在0到1之间，计算公式如下：

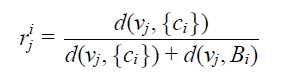
其中，d（v，S）表示v到S中任意一个顶点的距离的最小值，采用的是Dijkstra最短路径算法

（注：对于h和r的计算有点担心理解有偏差，截图附上此部分英文原文）

根据半径r构造基函数，为了得到更好的效果，将基函数构造为墨西哥草帽函数"

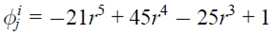
之所以选择这个函数是因为这个函数在坐标原点处连续，并且在原点处积分为0，不会引起模型的明显变化。

水印提取：

在进行水印提取之前, 可能需要对受攻击网格进行重定位或者重采样。当三维模型受到相似变换( 平移、旋转、一致放缩) 攻击时, 为了正确地提取水印,需要把模型带回原始的位置和尺度, 这是网格的重定位, 重定位( Registration ) 也称为对准、匹配。

重定位: 重定位可以理解为在两个模型间寻找一个变换, 使得两个模型间的"距离"最小

Get points v* on attacked mesh surface corresponding to original mesh vertices v

Use same basis functions f 1 … f m and hence same matrix B

Resampling choices:

• Closest point projection
• Ray-casting along local normal
• Global deformation of original

完成上述两步（视情况而定，不一定必须）后，可以从可疑网格中提取水印了，根据下列公式

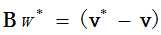
W* ：从可疑模型中提取出的水印

V* ：可疑网格中的顶点坐标

V ：原始网格中的顶点坐标

解决该最小二乘法问题可以求出W*

计算两者之间的相关性：

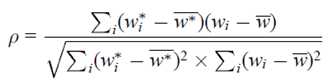
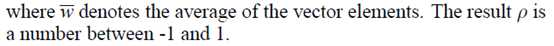
Pfp computed from r and m using Student‘s t-test

Declare watermark present if

Pfp < Pthresh ( e.g. Pthresh = 10-6 )

根据作者的实验，这种水印可以抵抗多种攻击，具有较强的鲁棒性。具体实验结果请参看原文。

Robust Mesh Watermarking

标签：

原文地址：http://www.cnblogs.com/scut-linmaojiang/p/4349476.html