poj1189 简单dp

标签：

http://poj.org/problem?id=1189

Description

有一个三角形木板,竖直立放，上面钉着n(n+1)/2颗钉子，还有(n+1)个格子（当n=5时如图1）。每颗钉子和周围的钉子的距离都等于d，每个格子的宽度也都等于d，且除了最左端和最右端的格子外每个格子都正对着最下面一排钉子的间隙。 
让一个直径略小于d的小球中心正对着最上面的钉子在板上自由滚落，小球每碰到一个钉子都可能落向左边或右边（概率各1/2），且球的中心还会正对着下一颗将要碰上的钉子。例如图2就是小球一条可能的路径。 
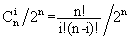我们知道小球落在第i个格子中的概率pi=pi=，其中i为格子的编号，从左至右依次为0,1,...,n。 
现在的问题是计算拔掉某些钉子后，小球落在编号为m的格子中的概率pm。假定最下面一排钉子不会被拔掉。例如图3是某些钉子被拔掉后小球一条可能的路径。 

Input

Output

Sample Input

5 2
*
   * .
  * * *
 * . * *
* * * * *

Sample Output

7/16

/**
poj1189 简单dp
题目大意：又是中文题~
解题思路； 总共会出现2^n种情况，我们一开始就假设有2^n个球在(1,1)点往下落。
           对于每一个没有挖掉的钉子(i,j)：dp[i+1][j]+=dp[i][j]/2; dp[i+1][j+1]+=dp[i][j]/2;
           对于挖掉的钉子(i,j)：dp[i+2][j+1]+=dp[i][j];
*/
#include <stdio.h>
#include <string.h>
#include <algorithm>
#include <iostream>
using namespace std;
typedef long long LL;

bool a[2555];
int n,m;
LL dp[55][55];

LL gcd(LL x,LL y)
{
    if(y==0)return x;
    return gcd(y,x%y);
}

int main()
{
    while(~scanf("%d%d",&n,&m))
    {
        int k=1;
        for(int i=1; i<=n; i++)
        {
            for(int j=1; j<=i; j++)
            {
                char str[12];
                scanf("%s",str);
                if(str[0]=='*')
                {
                    a[k++]=true;
                }
                else
                {
                    a[k++]=false;
                }
                //printf("%d\n",a[k-1]);
            }
            //puts("");
        }
        memset(dp,0,sizeof(dp));
        dp[1][1]=1LL<<n;
        for(int i=1; i<=n; i++)
        {
            int x=i*(i-1)/2;
            for(int j=1; j<=i; j++)
            {
                if(a[j+x])
                {
                    dp[i+1][j]+=dp[i][j]/2;
                    dp[i+1][j+1]+=dp[i][j]/2;
                }
                else
                {
                    dp[i+2][j+1]+=dp[i][j];
                }
            }
        }
        LL x=1LL<<n;
        LL y=dp[n+1][m+1];
        LL g=gcd(x,y);
        printf("%lld/%lld\n",y/g,x/g);
    }
    return 0;
}

poj1189 简单dp

标签：

原文地址：http://blog.csdn.net/lvshubao1314/article/details/44488743