标签：

Double Dealing

1 3
10 3
52 4
0 0

1
4
13

1. n张牌 (1,2,···,n) 按顺序发给k个人，再把牌收回，第1个人的放最上面，后面的依次放下面。继续发牌，收牌，问多少次后恢复原样。

2. 以 n=10,k=3 为例，4次后牌的次序恢复原样，如下：

第一次: 10  7  4   1   8   5   2   9   6   3
第二次: 3   2  1   10  9   8   7   6   5   4
第三次: 4   7  10  3   6   9   2   5   8   1
第四次: 1   2  3    4   5   6   7   8   9   10

3. 经过 1 次操作（发牌+收牌）后，下标变化情况如下：

原次序：1  2  3    4  5  6  7  8  9  10
操作后：4  7  10  3  6  9  2  5  8  1

4. 显然，该操作为一个置换，且为：

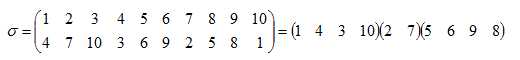
5. n 元数码上的任意置换 σ 都可唯一地表示成不相交的循环置换的乘积。

6. lcm(x,y)=xy/gcd(x,y).

7. lcm(x₁,x₂,···,x_n)=lcm(lcm(x₁,x₂,···,x_n-1),x_n).

8. 本题所求即为各循环置换的循环节的最小公倍数。以 n=10,k=3 为例，所求为 lcm(4,2,4)=4.

ac代码

#include<stdio.h>
#include<string.h>
#include<stdlib.h>
__int64 gcd(__int64 a,__int64 b)
{
	int t;
	if(a<b)
	{
		t=a;
		a=b;
		b=t;
	}
	if(b==0)
		return a;
	return gcd(b,a%b);
}
__int64 lcm(__int64 a,__int64 b)
{
	return a/gcd(a,b)*b;
}
int vis[100100],next[100100];
int main()
{
	int n,m;
	while(scanf("%d%d",&n,&m)!=EOF,n||m)
	{
		int i,j,k=n;
		if(n<=m)
		{
			printf("1\n");
			continue;
		}
		for(i=m;i>=1;i--)
		{
			for(j=i;j<=n;j+=m)
			{
				next[k--]=j;
			}
		}
		__int64 ans=1;
		memset(vis,0,sizeof(vis));
		for(i=1;i<=n;i++)
		{
			if(vis[i])
				continue;
			__int64 temp=next[i],res=1;
			while(temp!=i)
			{
				vis[temp]=1;
				temp=next[temp];
				res++;
			}
			ans=lcm(ans,res);
		}
		printf("%I64d\n",ans);
	}
}

HDOJ 4259 Double Dealing（置换群）

标签：

原文地址：http://blog.csdn.net/yu_ch_sh/article/details/44489241